
科目: 来源:2010-2011年北京市东城区九年级第二学期综合练习数学卷 题型:解答题
如图1,在△ABC中,AB=BC=5,AC="6." △ECD是△ABC沿CB方向平移得到的,连结AE,AC和BE相交于点O.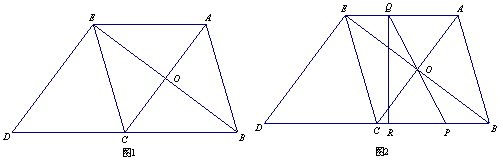
【小题1】(1)判断四边形ABCE是怎样的四边形,并证明你的结论;
【小题2】(2)如图2,P是线段BC上一动点(不与点B、C重合),连接PO并延长交线段AE于点Q,QR⊥BD,垂足为点R.
①四边形PQED的面积是否随点P的运动而发生变化?若变化,请说明理由;若不变,求出四边形PQED的面积;
②当线段BP的长为何值时,以点P、Q、R为顶点的三角形与△BOC相似?
查看答案和解析>>
科目: 来源:2011届安徽省长丰下塘实验中学九年级上学期期中数学卷 题型:解答题
如图,在Rt△ABC中,∠ACB=90º,AB=10,AC=6 ,点E、F分别是边AC、BC上的动点,过点E作ED⊥AB于点D,过点F作FG⊥AB于点G,DG的长始终为2.
,点E、F分别是边AC、BC上的动点,过点E作ED⊥AB于点D,过点F作FG⊥AB于点G,DG的长始终为2.
【小题1】当AD=3时,求DE的长;
【小题2】当点 E、F在边AC、BC上移动时,设
E、F在边AC、BC上移动时,设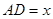 ,
,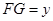 ,
,
求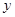 关于
关于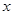 的函数解析式,并写出函数的定义域;
的函数解析式,并写出函数的定义域;
【小题3】在点E、F移动过 程中,△AED与△CEF能否相似,
程中,△AED与△CEF能否相似,
若能,求AD的长;若不能,请说明理由.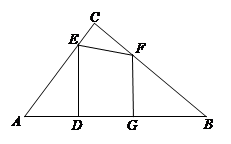
查看答案和解析>>
科目: 来源:2011届安徽省长丰下塘实验中学九年级上学期期中数学卷 题型:解答题
如图,已知△ABC中CEAB于E,BFAC于F,
求证:△AFE~△ABC
若时,若∠A=60°,求△AFE与△ABC面积之比。
查看答案和解析>>
科目: 来源:2011-2012学年九年级期末数学试卷 题型:解答题
如图,四边形ABCD是正方形,CE是∠BCD的外角∠DCF的平分线.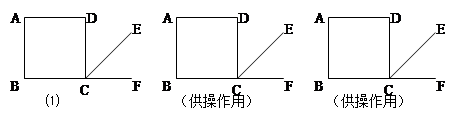
(如果需要,还可以继续操作、实验与测量)
【小题1】操作实验:将直角尺的直角顶点P在边BC上移动(与点B、C不重合),且一直角边经过点A,另一直角边与射线CE交于点Q,不断移动P点,同时测量线段PQ与线段PA的长度,完成下列表格(精确到0.1cm).
| | PA | PQ |
| 第一次 | | |
| 第二次 | | |
查看答案和解析>>
科目: 来源:2011-2012学年九年级期末数学试卷 题型:解答题
王华同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行12m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部.已知王华同学的身高是1.6m,两个路灯的高度都是9.6m.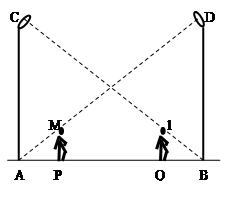
【小题1】求两个路灯之间的距离;(考查投影及相似三角形中的比例计算)
【小题2】当王华同学走到路灯BD处时,他在路灯AC下的影子长是多少?
查看答案和解析>>
科目: 来源:2011-2012年浙江省衢州华外九年级第一学期第三次质量检测数学卷 题型:解答题
(本题8分)如图,在一块三角形区域ABC中,∠C=90°,边AC=8m,BC=6m,现要在△ABC内建造一个矩形水池DEFG,如图的设计方案是使DE在AB上.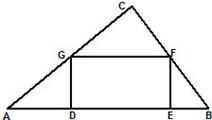
【小题1】(1)求△ABC中AB边上的高h;
【小题2】(2)设DG=x,水池DEFG的面积为S,求S关于x的函数关系式,当x取何值时,水池DEFG的面积S最大?
查看答案和解析>>
科目: 来源:2011-2012年浙江省萧浦沿中学九年级12月月考数学卷 题型:解答题
(本题12分)AB是⊙O的直径,点E是半圆上一动点(点E与点A、B都不重合),点C是BE延长线上的一点,且CD⊥AB,垂足为D,CD与AE交于点H,点H与点A不重合。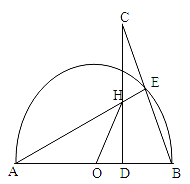
【小题1】(1)求证:△AHD∽△CBD
【小题2】(2)若CD=AB=2,求HD+HO的值。
查看答案和解析>>
科目: 来源:2011-2012年浙江省萧浦沿中学九年级12月月考数学卷 题型:解答题
(本题8分)如图,在Rt△ABC中,AC=4,BC=3.在Rt△ABC内并排放入(不重叠)n个小正方形纸片,使这些纸片的一边都在AB上,首尾两个正方形各有一个顶点D、E分别在AC、BC上,求小正方形的边长(用n的代数式表示)。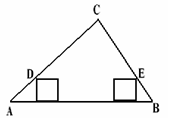
查看答案和解析>>
科目: 来源:2011-2012年山西省临汾市九年级第一学期期中考试数学卷 题型:解答题
已知:等腰梯形ABCD,AD∥BC,AB=DC=5,AD=6,BC=12,动点P从点D出发沿DC以每秒1个单位向终点C运动,点Q从点C出发沿CB以每秒2个单位向B运动,当点P到达C时,点Q随之停止运动,设点P运动的时间为t秒.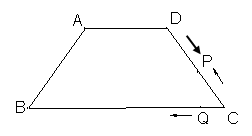
【小题1】(1)求梯形ABCD面积.
【小题2】(2)当PQ∥AB时,求t.
【小题3】(3) 当点P、Q、C三点构RT△时,求t值.
查看答案和解析>>
科目: 来源:2011-2012年山西省临汾市九年级第一学期期中考试数学卷 题型:解答题
如图测量电线杆AB的高度,发现电线杆的影子恰好落在土坡的坡面CD和地面BC上,量得CD="4" m,BC="10" m,CD与地面成30°角,且此时测得1m杆的影子长为2 m,则电线杆的高度约为多少m?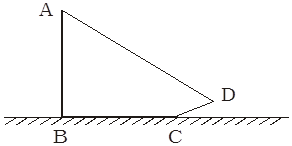
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com