
科目: 来源:2012届江苏泰兴实验初级中学九年级第二次模拟数学试卷(带解析) 题型:解答题
已知四边形ABCD的外接圆⊙O的半径为5,对角线AC与BD的交点为E,且AB2=AE·AC,BD=8,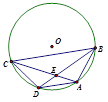
【小题1】判断△ABD的形状并说明理由;
【小题2】求△ABD的面积
查看答案和解析>>
科目: 来源:2012届江苏省泰兴市黄桥区九年级中考一模数学试卷(带解析) 题型:解答题
如图,梯形ABCD中,AB∥CD,∠ABC=90°,AB=8,CD=6,BC = 4,AB边上有一动点P(不与A、B重合),连结DP,作PQ⊥DP,使得PQ交射线BC于点E,设AP=x.
【小题1】当x为何值时,△APD是等腰三角形?
【小题2】若设BE=y,求y关于x的函数关系式
【小题3】若BC的长可以变化,在现在的条件下,是否存在点P,使得PQ经过点C?若存在,求出相应的AP的长;若不存在,请说明理由,并直接写出当BC的长在什么范围内时,可以存在这样的点P,使得PQ经过点C.

查看答案和解析>>
科目: 来源:2012届江苏省苏州市景范中学九年级中考二模数学试卷(带解析) 题型:解答题
如图,在锐角△ABC中,AC是最短边;以AC中点O为圆心, AC长为半径作⊙O,交BC于E,过O作OD∥BC交⊙O于D,连结AE、AD、DC.
AC长为半径作⊙O,交BC于E,过O作OD∥BC交⊙O于D,连结AE、AD、DC.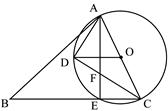
【小题1】求证:D是弧AE的中点;
【小题2】求证:∠DAO=∠B+∠BAD;
【小题3】若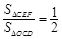 ,且AC=4,求CF的长.
,且AC=4,求CF的长.
查看答案和解析>>
科目: 来源:2012届山东宁津县中考二模数学卷(带解析) 题型:解答题
在△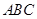 中,AD⊥BC,
中,AD⊥BC,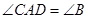
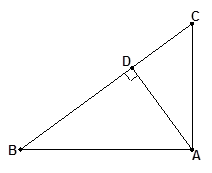
(1)利用尺规作图,作△ 外接圆⊙O;
外接圆⊙O;
(2)判断:AC和⊙O的位置关系,并说明理由;
(3)若AC=10,AD=8,求⊙O的直径;
查看答案和解析>>
科目: 来源:2012届福建厦门外国语学校九年级中考模拟数学试卷(带解析) 题型:解答题
如图,四边形ABCD为矩形,AB=4,AD=3,动点M、N分别从D、B同时出发,以1个单位/秒的速度运动,点M沿DA向终点A运动,点N沿BC向终点C运动。过点N作NP⊥BC,交AC于点P,连结MP。已知动点运动了 秒。
秒。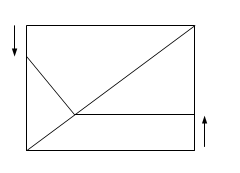
【小题1】请直接写出PN的长 ;(用含 的代数式表示)
的代数式表示)
【小题2】若0秒≤ ≤3秒,试求△MPA的面积S与时间
≤3秒,试求△MPA的面积S与时间 秒的函数关系式,并求S的最大值。
秒的函数关系式,并求S的最大值。
【小题3】若0秒≤ ≤3秒,△MPA能否与△PCN相似?若能,试求出相似时
≤3秒,△MPA能否与△PCN相似?若能,试求出相似时 的对应值;若不能,试说明理由。
的对应值;若不能,试说明理由。
查看答案和解析>>
科目: 来源:2012届江苏省泰州市海陵区九年级二模数学卷(带解析) 题型:解答题
等边△ABC边长为6,P为BC边上一点,∠MPN=60°,且PM、PN分别于边AB、AC交于点E、F.(1)如图1,当点P为BC的三等分点,且PE⊥AB时,判断△EPF的形状;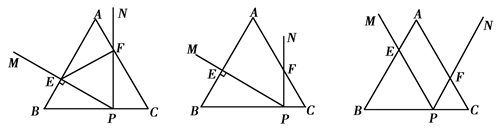
(2)如图2,若点P在BC边上运动,且保持PE⊥AB,设BP=x,四边形AEPF面积的y,求y与x的函数关系式,并写出自变量x的取值范围;
(3)如图3,若点P在BC边上运动,且∠MPN绕点P旋转,当CF=AE=2时,求PE的长.
查看答案和解析>>
科目: 来源:2012届江苏省泰州市海陵区九年级二模数学卷(带解析) 题型:解答题
如图,以△ABC的边AB为直径的⊙O与边BC交于点D,过点D作DE⊥AC,垂足为E,延长AB、ED交于点F,AD平分∠BAC.(1)求证:EF是⊙O的切线;(2)若AE=3,BF=2,求⊙O的半径.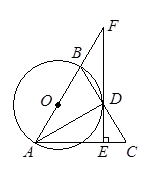
查看答案和解析>>
科目: 来源:2012届江苏镇江九年级5月中考模拟数学试卷(带解析) 题型:解答题
如图,在梯形ABCD中,AD∥BC,AD=3,DC=5,AB=4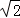 ,∠B=45°.动点M从B点出发沿线段BC以每秒2个单位长度的速度向终点C运动;动点N同时从C点出发沿线段CD以每秒1个单位长度的速度向终点D运动.设运动的时间为t秒.
,∠B=45°.动点M从B点出发沿线段BC以每秒2个单位长度的速度向终点C运动;动点N同时从C点出发沿线段CD以每秒1个单位长度的速度向终点D运动.设运动的时间为t秒.
【小题1】求BC的长
【小题2】当MN∥AB时,求t的值
【小题3】试探究:t为何值时,△MNC为等腰三角形.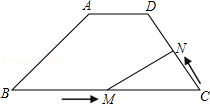
查看答案和解析>>
科目: 来源:2012届江苏镇江九年级第二次中考模拟数学试卷(带解析) 题型:解答题
如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,AC平分∠DAB.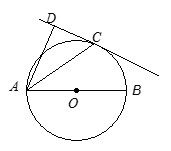
【小题1】求证:AD⊥DC
【小题2】若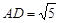 ,
, ,求
,求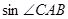 的值以及AB的长.
的值以及AB的长.
查看答案和解析>>
科目: 来源:2012届福建省泰宁县九年级学业质量检测考试数学试卷(带解析) 题型:解答题
如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,D、E分别是边AB、AC的中点,点P从点D出发沿DE方向运动,过点P作PQ⊥BC于Q,过点Q作QR‖BA交AC于R,当点Q与点C重合时,点P停止运动.
【小题1】求点D到BC的距离DH的长;
【小题2】设BQ=x, QR=y.
① 求y关于x的函数关系式(0≤x≤10);
② 是否存在点P,使△PQR为等腰三角形?若存在,求出所有满足要求的x的值;若不存在,请说明理由.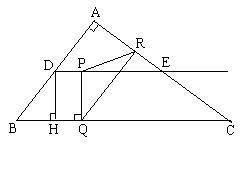
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com