
科目: 来源:2012年初中毕业升学考试(四川南充卷)数学(带解析) 题型:解答题
矩形ABCD中,AB=2AD,E为AD的中点,EF⊥EC交AB于点F,连接FC.
(1)求证:⊿AEF∽⊿DCE
(2)求tan∠ECF的值.
查看答案和解析>>
科目: 来源:2012年初中毕业升学考试(上海卷)数学(带解析) 题型:解答题
己知:如图,在菱形ABCD中,点E、F分别在边BC、CD,∠BAF=∠DAE,AE与BD交于点G.
(1)求证:BE=DF;
(2)当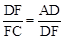 时,求证:四边形BEFG是平行四边形.
时,求证:四边形BEFG是平行四边形.
查看答案和解析>>
科目: 来源:2012年初中毕业升学考试(山东临沂卷)数学(带解析) 题型:解答题
如图,点A.F、C.D在同一直线上,点B和点E分别在直线AD的两侧,且
AB=DE,∠A=∠D,AF=DC.
(1)求证:四边形BCEF是平行四边形,
(2)若∠ABC=90°,AB=4,BC=3,当AF为何值时,四边形BCEF是菱形.
查看答案和解析>>
科目: 来源:2012届浙江省乐清市盐盘一中中考仿真联考数学试卷(带解析) 题型:解答题
直角梯形ABCD中,AD∥BC,AB=AD=3,边BC, AB分别在x轴和y轴上,已知点C的坐标分别为(4,0)。动点P从B点出发,以每秒1个单位的速度沿BC方向作匀速直线运动,同时点Q从D点出发,以与P点相同的速度沿DA方向运动,当Q点运动到A点时, P,Q两点同时停止运动。设点P运动时间为t,
(1)求线段CD的长。
(2) 连接PQ交直线AC于点E,当AE : EC="1" : 2时,求t的值,并求出此时△PEC的面积。
(3) 过Q点作垂直于AD的射线交AC于点M,交BC于点N,连接PM,
①是否存在某一时刻,使以M、P、C三点为顶点的三角形是等腰三角形?若存在 ,求出此时t的值;若不存在,请说明理由;
②当t= 时,点P、M、D在同一直线上。(直接写出)

|
查看答案和解析>>
科目: 来源:2012届江苏省江阴初级中学九年级5月中考模拟数学试卷(带解析) 题型:解答题
如图,在直角坐标平面中,O为原点,A(0,6),B(8,0)。点P从点A出发,以每秒2个单位长度的速度沿射线AO方向运动,点Q从点B出发,以每秒一个单位长度的速度沿x轴正方向运动,P,Q两动点同时出发,设移动时间为t(t>0)秒.
(1)在点P,Q的运动过程中,当点P在AO的延长线上时,若△POQ与△AOB相似,求t的值;
(2)如图2,当直线PQ与线段AB交于点M,且 时,求直线PQ的解析式;
时,求直线PQ的解析式;
(3)以点O为圆心,OP长为半径画圆⊙O,以点B为圆心,BQ长为半径画⊙B,讨论⊙O和⊙B的位置关系,并直接写出相应t的取值范围.
查看答案和解析>>
科目: 来源:2012届重庆巴南区全善学校(先华中学)九年级第三次月考数学试卷(带解析) 题型:解答题
如图,点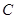 ,
,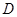 在线段
在线段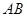 上,且
上,且 是等边三角形。
是等边三角形。
① 若 ·
· ,求证
,求证 ∽
∽ 。
。
② 当 ∽
∽ 时,试求
时,试求 的度数。
的度数。
查看答案和解析>>
科目: 来源:2012届浙江省德清县士林中学中考模拟考试数学试卷(带解析) 题型:解答题
△ABC中,AB=1,AC=2,D是BC中点,AE平分∠BAC交BC于E,且DF∥AE.求CF的长.
查看答案和解析>>
科目: 来源:2012届浙江省德清县士林中学中考模拟考试数学试卷(带解析) 题型:解答题
已知:如图,O正方形ABCD的中心,BE平分∠DBC,交DC于点E,延长BC到点F ,使CF=CE,连结DF,交BE的延长线于点G,连结OG.
⑴ 求证:△BCE≌△DCF;
⑵ OG与BF有什么数量关系?证明你的结论;
⑶ 若GE·GB=4-2 ,求 正方形ABCD的面积.
,求 正方形ABCD的面积.
查看答案和解析>>
科目: 来源:2012届浙江省杭州市上城区中考二模数学试卷(带解析) 题型:解答题
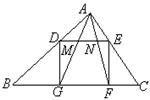
如图,△ABC中,∠BAC=90°,正方形的一边GF在BC上,其余两个顶点D,E分别在AB,AC上.连接AG,AF分别交DE于M,N两点.
(1)求证: .
.
(2)求证: .
.
(3)若AB=AC=2,求MN的长.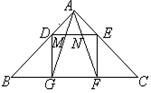
查看答案和解析>>
科目: 来源:2012届浙江省杭州市上城区中考二模数学试卷(带解析) 题型:解答题
如图①,P为△ABC内一点,连接PA,PB,PC,在△PAB,△PBC和△PAC中,如果存在一个三角形与△ABC相似,那么就称P为△ABC的自相似点.
已知△ABC中,∠A<∠B<∠C
(1)利用直尺和圆规,在图②中作出△ABC的自相似点P(不写作法,但需保留作图痕迹);
(2)若△ABC的三内角平分线的交点P是该三角形的自相似点,求该三角形三个内角的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com