
科目: 来源:2012-2013学年浙江省八里店一中九年级第二学期期中考试数学试卷(带解析) 题型:解答题
如图, 中,
中, ,
,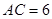 ,过点
,过点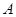 作
作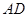 ∥
∥ ,点
,点 、
、 分别是射线
分别是射线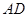 、线段
、线段 上的动点,且
上的动点,且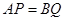 ,过点
,过点 作
作 ∥
∥ 交线段
交线段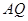 于点
于点 ,联接
,联接 ,设
,设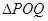 面积为
面积为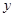 ,
,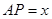 .
.
(1)用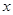 的代数式表示
的代数式表示 ;
;
(2)求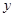 与
与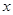 的函数关系式,并写出定义域;
的函数关系式,并写出定义域;
(3)联接 ,若
,若 与
与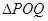 相似,求
相似,求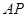 的长.
的长.
查看答案和解析>>
科目: 来源:2012-2013学年浙江省八里店二中八年级下学期期中考试数学试卷(带解析) 题型:解答题
如图,四边形OABE中,∠AOE=∠BEO=90°,OA=3, OE==4,BE=1,点C,D是边OE(与端点O、E不重合)上的两个动点且CD=1.
(1)求边AB的长;
(2)当△AOD与△BCE相似时,求OD的长.
(3)连结AC与BD相交于点P,设OD=x,△PDC的面积记为y,求y关于x的函数关系式,并写出x的取值范围.
查看答案和解析>>
科目: 来源:2013届广东省中山市三校九年级第一次联合模拟考试数学试卷(带解析) 题型:解答题
如图,在边长均为1的小正方形网格纸中,△ 的顶点
的顶点 、
、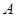 、
、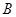 均在格点上,且
均在格点上,且 是直角坐标系的原点,点
是直角坐标系的原点,点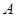 在
在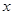 轴上.
轴上.
(1)以O为位似中心,将△ 放大,使得放大后的△
放大,使得放大后的△ 与△
与△ 对应线段的比为2∶1,画出△
对应线段的比为2∶1,画出△ .(所画△
.(所画△ 与△
与△ 在原点两侧).
在原点两侧).
(2)求出线段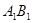 所在直线的函数关系式.
所在直线的函数关系式.
查看答案和解析>>
科目: 来源:2012-2013学年湖北省宜昌中学八年级下学期期中考试数学试卷(带解析) 题型:解答题
如果一个矩形的宽与长的比是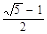 ,那么这个矩形就是一个黄金矩形。在黄金矩形ABCD的内部作一个正方形CDFE后,得到一个新的矩形ABFE,那么ABFE也是黄金矩形吗?
,那么这个矩形就是一个黄金矩形。在黄金矩形ABCD的内部作一个正方形CDFE后,得到一个新的矩形ABFE,那么ABFE也是黄金矩形吗? 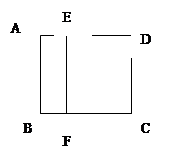
查看答案和解析>>
科目: 来源:2012-2013学年浙江省湖州十二中七年级第二学期期中考试数学试卷(带解析) 题型:解答题
如图,在直角梯形ABCD中,AB∥DC,∠D=90o,AC⊥BC,AB=10cm,BC=6cm,F点以2cm/秒的速度在线段AB上由A向B匀速运动,E点同时以1cm/秒的速度在线段BC上由B向C匀速运动,设运动时间为t秒(0<t<5).
(1)求证:△ACD∽△BAC;
(2)求DC的长;
(3)设四边形AFEC的面积为y,求y 关于t的函数关系式,并求出y的最小值.
查看答案和解析>>
科目: 来源:2012-2013学年度安徽怀远第一学期九年级期末质量检测数学试卷(带解析) 题型:解答题
如下图,△ABC在方格纸中.
(1)请在方格纸上建立平面直角坐标系,使A(3,3)、C(6,2),并求出B点坐标;
(2)以原点O为位似中心,相似比为2,在第一象限内将△ABC放大,
画出放大后的图形△A′B′C′;
查看答案和解析>>
科目: 来源:2012-2013学年吉林镇赉镇赉镇中学九年级下第一次综合测试数学试卷(带解析) 题型:解答题
数学课上,李老师出示范了如下框中的题目.
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论
当点E为AB的中点时,如图1,确定线段AE与DB的大小关系.请你直接写出结论:AE DB(填“>”、“<”或“=”);
(2)特例启发,解答题目
解:题目中,AE与DB的大小关系是:AE DB(填“>”、“<”或“=”).理由如下:
如图2过点E作EF∥BC,交AC于点F;(请你完成以下解答过程)
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为1,AE=2,求CD的长(请你直接写出结果).
查看答案和解析>>
科目: 来源:2013届北京市龙文教育九年级第一次中考模拟数学试卷(带解析) 题型:解答题
在Rt△ABC中,∠ACB=90°,tan∠BAC= . 点D在边AC上(不与A,C重合),连结BD,F为BD中点.
. 点D在边AC上(不与A,C重合),连结BD,F为BD中点.
(1)若过点D作DE⊥AB于E,连结CF、EF、CE,如图1.设 ,则k = ;
,则k = ;
(2)若将图1中的△ADE绕点A旋转,使得D、E、B三点共线,点F仍为BD中点,如图2所示.求证:BE-DE=2CF;
(3)若BC=6,点D在边AC的三等分点处,将线段AD绕点A旋转,点F始终为BD中点,求线段CF长度的最大值.
查看答案和解析>>
科目: 来源:2013届浙江省温州市育英学校九年级第二学期开学考试数学试卷(带解析) 题型:解答题
网格中每个小正方形的边长都是1.

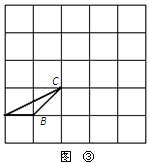
(1)将图①中的格点三角形ABC平移,使点A平移至点A`,画出平移后的三角形;
(2)在图②中画一个格点三角形DEF,使△DEF∽△ABC,且相似比为2∶1;
(3)在图③中画一个格点三角形PQR,使△PQR∽△ABC,且相似比为 ∶1.
∶1.
(4)图②与图③中的△DEF与△PQR的相似比为
查看答案和解析>>
科目: 来源:2013届浙江省温州市育英学校九年级第二学期开学考试数学试卷(带解析) 题型:解答题
如图,等腰三角形ABC中,若∠A=∠B=∠DPE,
(1)求证:△APD∽△BEP;
(2)若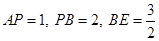 ,试求出AD的长.
,试求出AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com