
科目: 来源:2013届江苏省扬州市宝应县九年级中考网上阅卷适应性调研(一模)数学试卷(带解析) 题型:解答题
如图,在△ABD和△ACE中,AB=AD,AC=AE,∠BAD=∠CAE,连接BC、DE相交于点F,BC与AD相交于点G.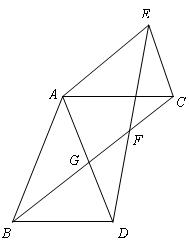
(1)求证:BC=DE;
(2)如果∠ABC=∠CBD ,那么线段FD是线段FG和FB的比例中项吗?为什么?
查看答案和解析>>
科目: 来源:2013届江苏省如皋市九年级中考模拟数学试卷(带解析) 题型:解答题
如图,矩形ABCD中,AB="10" cm,BC="6" cm.现有两个动点P,Q分别从A,B同时出发,点P在线段AB上沿AB方向作匀速运动,点Q在线段BC上沿BC方向作匀速运动,已知点P的运动速度为1 cm/s,运动时间为t s.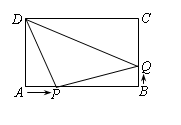
(1)设点Q的运动速度为 cm/s.
cm/s.
①当△DPQ的面积最小时,求t的值;
②当△DAP∽△QBP相似时,求t的值.
(2)设点Q的运动速度为a cm/s,问是否存在a的值,使得△DAP与△PBQ和△QCD这两个三角形都相似?若存在,请求出a的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源:2013年四川省乐山市沙湾区九年级调研考试数学试卷(带解析) 题型:解答题
如图,在航线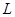 的两侧分别有观测点
的两侧分别有观测点 和
和 ,点
,点 到航线
到航线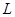 的距离为
的距离为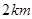 ,点
,点 位于点
位于点 北偏东
北偏东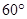 方向且与
方向且与 相距
相距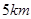 处. 现有一艘轮船正沿该航线自西向东航行,在
处. 现有一艘轮船正沿该航线自西向东航行,在 点观测到点
点观测到点 位于南偏东
位于南偏东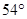 方向,航行
方向,航行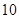 分钟后,在
分钟后,在 点观测到点
点观测到点 位于北偏东
位于北偏东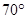 方向.
方向.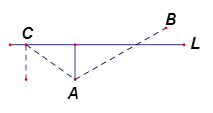
(1)求观测点 到航线
到航线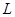 的距离;
的距离;
(2)该轮船航线的速度(结果精确到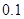 )
)
参考数据: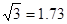 ,
,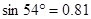 ,
,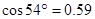 ,
,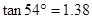 ,
,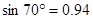 ,
,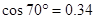 ,
,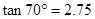 .
.
查看答案和解析>>
科目: 来源:2013届宁夏青铜峡市九年级联考数学试卷(带解析) 题型:解答题
已知:如图①,在 中,
中, ,
,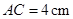 ,
,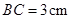 ,点
,点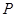 由
由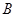 出发沿
出发沿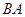 方向向点
方向向点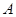 匀速运动,速度为1cm/s;点
匀速运动,速度为1cm/s;点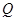 由
由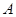 出发沿
出发沿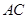 方向向点
方向向点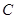 匀速运动,速度为2cm/s;连接
匀速运动,速度为2cm/s;连接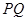 .若设运动的时间为
.若设运动的时间为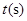 (
(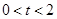 ),解答下列问题:
),解答下列问题:
(1)当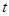 为何值时,
为何值时,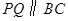 ?
?
(2)设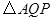 的面积为
的面积为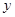 (
(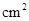 ),求
),求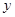 与
与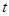 之间的函数关系式;
之间的函数关系式;
(3)如图②,连接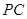 ,并把
,并把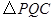 沿
沿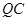 翻折,得到四边形
翻折,得到四边形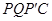 ,那么是否存在某一时刻
,那么是否存在某一时刻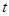 ,使四边形
,使四边形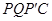 为菱形?若存在,求出此时
为菱形?若存在,求出此时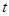 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目: 来源:2013届江苏省仪征市九年级第二次模拟考试数学试卷(带解析) 题型:解答题
已知:把 和
和 按如图(1)摆放(点
按如图(1)摆放(点 与点
与点 重合),点
重合),点 、
、 (
( )、
)、 在同一条直线上.
在同一条直线上. ,
, ,
,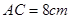 ,
, ,
, .如图(2),
.如图(2), 从图(1)的位置出发,以
从图(1)的位置出发,以 的速度沿
的速度沿 向
向 匀速移动,在
匀速移动,在 移动的同时,点
移动的同时,点 从
从 的顶点
的顶点 出发,以2 cm/s的速度沿
出发,以2 cm/s的速度沿 向点
向点 匀速移动.当
匀速移动.当 的顶点
的顶点 移动到
移动到 边上时,
边上时, 停止移动,点
停止移动,点 也随之停止移动.
也随之停止移动. 与
与 相交于点
相交于点 ,连接
,连接 ,设移动时间为
,设移动时间为
 .
.

(1)当 为何值时,点
为何值时,点 在线段
在线段 的垂直平分线上?
的垂直平分线上?
(2)连接 ,设四边形
,设四边形 的面积为
的面积为 ,求
,求 与
与 之间的函数关系式;是否存在某一时刻
之间的函数关系式;是否存在某一时刻 ,使面积
,使面积 最小?若存在,求出
最小?若存在,求出 的最小值;若不存在,说明理由.
的最小值;若不存在,说明理由.
(3)是否存在某一时刻 ,使
,使 、
、 、
、 三点在同一条直线上?若存在,求出此时
三点在同一条直线上?若存在,求出此时 的值;若不存在,说明理由.(图(3)供同学们做题使用)
的值;若不存在,说明理由.(图(3)供同学们做题使用)
查看答案和解析>>
科目: 来源:2012-2013学年山东省聊城地区八年级下学期期中考试数学试卷(带解析) 题型:解答题
如图,△ABC是一张锐角三角形的硬纸片,AD是边BC上的高,BC=40cm,AD=30cm.从这张硬纸片上剪下一个长HG是宽HE的2倍的矩形EFGH,使它的一边EF在BC上,顶点G、H分别在AC、AB上,高AD与HG的交点为M.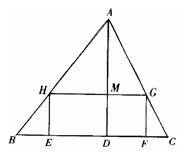
(1)求证: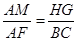 ;
;
(2)求这个矩形EFGH的周长.
查看答案和解析>>
科目: 来源:2012-2013学年山东省聊城地区八年级下学期期中考试数学试卷(带解析) 题型:解答题
在Rt△ABC中,∠C=900,D、E分别为AB、BC上的点,且BD·AB=BE·BC.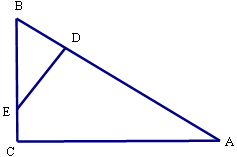
(1)△ABC与△EBD是否相似,为什么?
(2)ED与AB是否垂直,为什么?
查看答案和解析>>
科目: 来源:2013届江苏省兴化市戴瑶中学九年级一模数学试卷(带解析) 题型:解答题
如图,点P是菱形ABCD的对角线BD上一点,
连结CP并延长,交AD于E,交BA的延长线于点F.试问: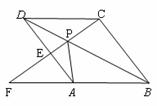
(1)图中△APD与哪个三角形全等?并说明理由.
(2)猜想:线段PC、PE、PF之间存在什么关系?并说明理由.
查看答案和解析>>
科目: 来源:2013年江苏省兴化市安丰中学九年级一模数学试卷(带解析) 题型:解答题
如图,四边形ABCD是正方形, 点G是BC上任意一点,DE⊥AG于点E,BF⊥AG于点F. 
(1) 求证:DE-BF = EF.
(2) 当点G为BC边中点时, 试探究线段EF与GF之间的数量关系, 并说明理由.
(3) 若点G为CB延长线上一点,其余条件不变.请画出图形,写出此时DE、BF、EF之间的数量关系(不需要证明).
查看答案和解析>>
科目: 来源:2013届上海市虹口区中考二模数学试卷(带解析) 题型:解答题
在Rt△ABC中,∠A=90°,AB=6,AC=8,点D为边BC的中点,DE⊥BC交边AC于点E,点P为射线AB上一动点,点Q为边AC上一动点,且∠PDQ=90°. 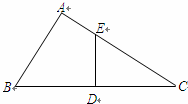
(1)求ED、EC的长;
(2)若BP=2,求CQ的长;
(3)记线段PQ与线段DE的交点为点F,若△PDF为等腰三角形,求BP的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com