
科目: 来源:2013-2014学年广东省广州市海珠区九年级上学期期末数学试卷(解析版) 题型:解答题
在10×10正方形网格中,每个小正方形的边长均为1个单位.
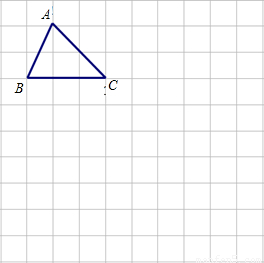
(1)把△ABC,绕着点C逆时针旋转90°,得到△A1B1C,请画出△A1B1C;
(2)选择点C为对称中心,请画出与△ABC关于点C对称的△A2B2C.(不要求写出作法)
查看答案和解析>>
科目: 来源:2013-2014学年广东省广州市海珠区九年级上学期期末数学试卷(解析版) 题型:解答题
某中学举行“中国梦,我的梦”演讲比赛,九年级(1)班的班长和学习委员都想去,于是他们用摸球游戏决定谁去参加,游戏规则是:在一个不透明的袋子里有除数字外完全相同的4个小球,上面分别标有数字1,2,3,4,一人先从袋中随机摸出一个小球,另一个人再从袋中剩下的3个小球中随机摸出一个小球。
(1)请列出所有可能出现的结果;(可考虑用树形图、列表等方法)
(2)若摸出的两个小球上的数字和为偶数,则班长去参赛,请问他能如愿的概率是多少?
查看答案和解析>>
科目: 来源:2013-2014学年广东省广州市海珠区九年级上学期期末数学试卷(解析版) 题型:解答题
雅安地震牵动全国人民的心,某单位开展了“一方有难,八方支援”赈灾捐款活动,第一天收到捐款10000元,第三天收到捐款12100元。
(1)如果第二天,第三天收到捐款的增长率相同,求捐款的平均增长率;
(2)按照(1)中收到捐款的增长率速度,第四天该单位能收到多少元的捐款?
查看答案和解析>>
科目: 来源:2013-2014学年广东省广州市海珠区九年级上学期期末数学试卷(解析版) 题型:解答题
如图,已知⊙O的半径为4,CD为⊙O的直径,AC为⊙O的弦,B为CD延长线上的一点,∠ABC=30°,且AB=AC。

(1)求证:AB是⊙O的切线;
(2)求弦AC的长;
(3)求图中阴影部分的面积。
查看答案和解析>>
科目: 来源:2013-2014学年广东省广州市海珠区九年级上学期期末数学试卷(解析版) 题型:解答题
已知抛物线y=x²-4x+3.
(1)该抛物线的对称轴是 ,顶点坐标 ;
(2)将该抛物线向上平移2个单位长度,再向左平移3个单位长度得到新的二次函数图像,请写出相应的解析式,并用列表,描点,连线的方法画出新二次函数的图像;
|
x |
… |
|
|
|
|
|
… |
|
y |
… |
|
|
|
|
|
… |
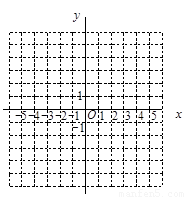
(3)新图像上两点A(x1,y1),B(x2,y2),它们的横坐标满足<-2,且-1<<0,试比较y1,y2,0三者的大小关系.
查看答案和解析>>
科目: 来源:2013-2014学年广东省广州市海珠区九年级上学期期末数学试卷(解析版) 题型:解答题
如图,点C在以AB为直径的半圆O上,以点A为旋转中心,以∠β(0°<β<90°)为旋转角度将B旋转到点D,过点D作DE⊥AB于点E,交AC于点F,过点C作圆O的切线交DE于点G。

(1)求证:∠GCA=∠OCB;
(2)设∠ABC=m°,求∠DFC的值;
(3)当G为DF的中点时,请探究∠β与∠ABC的关系,并说明理由。
查看答案和解析>>
科目: 来源:2013-2014学年广东省广州市海珠区九年级上学期期末数学试卷(解析版) 题型:解答题
二次函数y=ax²-6ax+c(a>0)的图像抛物线过点C(0,4),设抛物线的顶点为D。

(1)若抛物线经过点(1,-6),求二次函数的解析式;
(2)若a=1时,试判断抛物线与x轴交点的个数;
(3)如图所示A、B是⊙P上两点,AB=8,AP=5。且抛物线过点A(x1,y1),B(x2,y2),并有AD=BD。设⊙P上一动点E(不与A、B重合),且∠AEB为锐角,若<a≤1时,请判断∠AEB与∠ADB的大小关系,并说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com