
科目: 来源:2013-2014学年北京四中初三第一学期期中考试数学试卷(解析版) 题型:解答题
如图,为了测量某建筑物AB的高度,在平地上C处测得建筑物顶端A的仰角为30°,沿CB方向前进(9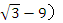 m到达D处,在D处测得建筑物顶端A的仰角为45°,求该建筑物AB的高度
m到达D处,在D处测得建筑物顶端A的仰角为45°,求该建筑物AB的高度
查看答案和解析>>
科目: 来源:2013-2014学年北京四中初三第一学期期中考试数学试卷(解析版) 题型:解答题
已知抛物线y=x2-2kx+3k+4.
(1)顶点在y轴上时,k的值为_________.
(2)顶点在x轴上时,k的值为_________.
(3)抛物线经过原点时,k的值为_______.
查看答案和解析>>
科目: 来源:2013-2014学年北京四中初三第一学期期中考试数学试卷(解析版) 题型:解答题
已知二次函数y=-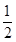 x2-x
x2-x .
.

(1)在给定的直角坐标系中,画出这个函数的图象;
(2)根据图象,写出当y<0时,x的取值范围;
(3)若将此图象沿x轴向右平移3个单位,请写出平移后图象所对应的函数关系式.
查看答案和解析>>
科目: 来源:2013-2014学年北京四中初三第一学期期中考试数学试卷(解析版) 题型:解答题
已知:如图,在△ABC中,AD是边BC上的高,E为边AC的中点,BC=14,AD=12,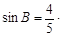

求:(1)线段DC的长;
(2)tan∠EDC的值.
查看答案和解析>>
科目: 来源:2013-2014学年北京四中初三第一学期期中考试数学试卷(解析版) 题型:解答题
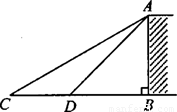
如图,直角△ABC中,∠C=90°,AB=2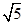 ,sinB=
,sinB=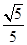 ,点P为边BC上一动点,PD∥AB,PD交AC于点D,连结AP.
,点P为边BC上一动点,PD∥AB,PD交AC于点D,连结AP.

(1)求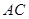 、
、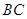 的长;
的长;
(2)设 的长为
的长为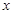 ,
, 的面积为
的面积为 .当
.当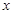 为何值时,
为何值时, 最大并求出最大值.
最大并求出最大值.
查看答案和解析>>
科目: 来源:2013-2014学年北京四中初三第一学期期中考试数学试卷(解析版) 题型:解答题
如图,直线y=3x和y=2x分别与直线x=2相交于点A、B,将抛物线y=x 2沿线段OB移动,使其顶点始终在线段OB上,抛物线与直线x=2相交于点C,设△AOC的面积为S,求S的取值范围.

查看答案和解析>>
科目: 来源:2013-2014学年北京四中初三第一学期期中考试数学试卷(解析版) 题型:解答题
某商品的进价为每件40元,售价为每件50元,每个月可卖出210件;如果每件商品的售价每上涨1元,则每个月少卖10件(每件售价不能高于65元).
设每件商品的售价上涨 元(
元( 为正整数),每个月的销售利润为
为正整数),每个月的销售利润为 元.
元.
(1)求 与
与 的函数关系式并直接写出自变量
的函数关系式并直接写出自变量 的取值范围;
的取值范围;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
(3)每件商品的售价定为多少元时,每个月的利润恰为2200元?根据以上结论,请你直接写出售价在什么范围时,每个月的利润不低于2200元?
查看答案和解析>>
科目: 来源:2013-2014学年北京四中初三第一学期期中考试数学试卷(解析版) 题型:解答题
当抛物线的解析式中含有字母系数时,随着系数中的字母取值的不同,抛物线的顶点坐标也将发生变化.例如:由抛物线y=x2-2mx+m2+2m-1①有y=(x-m)2+2m-1②,
所以抛物线顶点坐标为(m,2m-1),即x=m③,y=2m-1④.
当m的值变化时,x,y的值也随之变化,因而y的值也随x值的变化而变化.
将③代入④,得y=2x-1⑤.可见,不论m取任何实数,抛物线顶点的纵坐标y和横坐标x都满足关系式:y=2x-1;
根据上述阅读材料提供的方法,确定点(-2m, m-1)满足的函数关系式为_______.
(2)根据阅读材料提供的方法,确定抛物线 顶点的纵坐标y与横坐标x之间的关系式.
顶点的纵坐标y与横坐标x之间的关系式.
查看答案和解析>>
科目: 来源:2013-2014学年北京四中初三第一学期期中考试数学试卷(解析版) 题型:解答题
已知二次函数
(1)求证:不论a为何实数,此函数图象与x轴总有两个交点.
(2)设a<0,当此函数图象与x轴的两个交点的距离为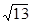 时,求出此二次函数的解析式.
时,求出此二次函数的解析式.
(3)在(2)的条件下,若此二次函数图象与x轴交于A、B两点,在函数图象上是否存在点P,使得△PAB的面积为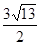 ,若存在求出P点坐标,若不存在请说明理由。
,若存在求出P点坐标,若不存在请说明理由。
查看答案和解析>>
科目: 来源:2013-2014学年北京四中初三第一学期期中考试数学试卷(解析版) 题型:解答题
已知:∠ACD=90°,MN是过点A的直线,AC=DC,DB⊥MN于点B,如图(1).易证BD+AB= CB,过程如下:过点C作CE⊥CB于点C,与MN交于点E
CB,过程如下:过点C作CE⊥CB于点C,与MN交于点E
∵∠ACB+∠BCD=90°,∠ACB+∠ACE=90°,∴∠BCD=∠ACE.
∵四边形ACDB内角和为360°,∴∠BDC+∠CAB=180°.
∵∠EAC+∠CAB=180°,∴∠EAC=∠BDC.
又∵AC=DC,∴△ACE≌△DCB,∴AE=DB,CE=CB,∴△ECB为等腰直角三角形,∴BE= CB.
CB.
又∵BE=AE+AB,∴BE=BD+AB,∴BD+AB= CB.
CB.
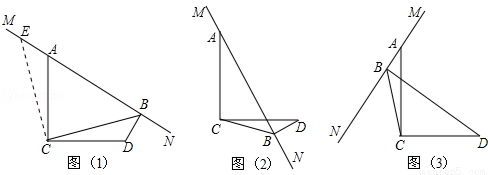
(1)当MN绕A旋转到如图(2)和图(3)两个位置时,其它条件不变,则BD、AB、CB满足什么样关系式,请写出你的猜想,并对图(2)给予证明.
(2)MN在绕点A旋转过程中,当∠BCD=30°,BD= 时,则CB=__________.
时,则CB=__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com