科目： 来源：第3章《圆》中考题集（41）：3.5 直线和圆的位置关系（解析版） 题型：解答题

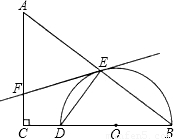
如图，在△ABC中，∠C=90°，AC=3，BC=4.0为BC边上一点，以0为圆心，OB为半径作半圆与BC边和AB边分别交于点D、点E，连接DE．
（1）当BD=3时，求线段DE的长；
（2）过点E作半圆O的切线，当切线与AC边相交时，设交点为F．求证：△FAE是等腰三角形．

科目： 来源：第3章《圆》中考题集（41）：3.5 直线和圆的位置关系（解析版） 题型：解答题

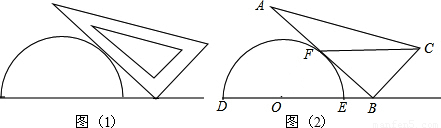
将一个量角器和一个含30度角的直角三角板如图（1）放置，图（2）是由它抽象出的几何图形，其中点B在半圆O的直径DE的延长线上，AB切半圆O于点F，且BC=OD．
（1）求证：DB∥CF；
（2）当OD=2时，若以O、B、F为顶点的三角形与△ABC相似，求OB．

科目： 来源：第3章《圆》中考题集（41）：3.5 直线和圆的位置关系（解析版） 题型：解答题

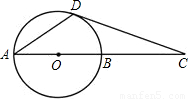
如图，AB是⊙O的直径，点C在AB的延长线上，CD与⊙O相切于点D，∠C=20度．求∠CDA的大小．

科目： 来源：第3章《圆》中考题集（41）：3.5 直线和圆的位置关系（解析版） 题型：解答题

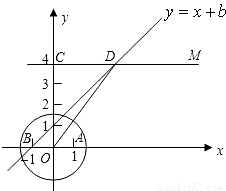
在直角坐标平面内，O为原点，点A的坐标为（1，0），点C的坐标为（0，4），直线CM∥x轴（如图所示）．点B与点A关于原点对称，直线y=x+b（b为常数）经过点B，且与直线CM相交于点D，连接OD．
（1）求b的值和点D的坐标；
（2）设点P在x轴的正半轴上，若△POD是等腰三角形，求点P的坐标；
（3）在（2）的条件下，如果以PD为半径的圆P与圆O外切，求圆O的半径．

科目： 来源：第3章《圆》中考题集（41）：3.5 直线和圆的位置关系（解析版） 题型：解答题

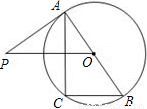
如图，已知AB是⊙O的直径，过点O作弦BC的平行线，交过点A的切线AP于点P，连接AC．
（1）求证：△ABC∽△POA；
（2）若OB=2，OP=，求BC的长．

科目： 来源：第3章《圆》中考题集（41）：3.5 直线和圆的位置关系（解析版） 题型：解答题

已知，如图，BC是以线段AB为直径的⊙O的切线，AC交⊙O于点D，过点D作弦DE⊥AB，垂足为点F，连接BD、BE．
（1）仔细观察图形并写出四个不同的正确结论：①______，②______，③______，④______（不添加其它字母和辅助线，不必证明）；
（2）∠A=30°，CD=，求⊙O的半径r．

科目： 来源：第3章《圆》中考题集（41）：3.5 直线和圆的位置关系（解析版） 题型：解答题

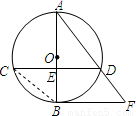
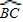
已知：如图，⊙O的直径AB与弦CD相交于E，=，⊙O的切线BF与弦AD的延长线相交于点F．
（1）求证：CD∥BF．
（2）连接BC，若⊙O的半径为4，cos∠BCD=，求线段AD、CD的长．

科目： 来源：第3章《圆》中考题集（41）：3.5 直线和圆的位置关系（解析版） 题型：解答题

如图，半圆的直径AB=10，点C在半圆上，BC=6．
（1）求弦AC的长；
（2）若P为AB的中点，PE⊥AB交AC于点E，求PE的长．

科目： 来源：第3章《圆》中考题集（41）：3.5 直线和圆的位置关系（解析版） 题型：解答题

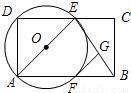
如图，矩形ABCD中，AB=5，AD=3．点E是CD上的动点，以AE为直径的⊙O与AB交于点F，过点F作FG⊥BE于点G．
（1）当E是CD的中点时：
①tan∠EAB的值为______；
②证明：FG是⊙O的切线；
（2）试探究：BE能否与⊙O相切？若能，求出此时DE的长；若不能，请说明理由．

科目： 来源：第3章《圆》中考题集（42）：3.5 直线和圆的位置关系（解析版） 题型：解答题

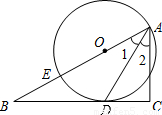
如图，已知点E在△ABC的边AB上，以AE为直径的⊙O与BC相切于点D，且AD平分∠BAC．
求证：AC⊥BC．