相关习题
0 125521 125529 125535 125539 125545 125547 125551 125557 125559 125565 125571 125575 125577 125581 125587 125589 125595 125599 125601 125605 125607 125611 125613 125615 125616 125617 125619 125620 125621 125623 125625 125629 125631 125635 125637 125641 125647 125649 125655 125659 125661 125665 125671 125677 125679 125685 125689 125691 125697 125701 125707 125715 366461
科目:
来源:第2章《二次函数》常考题集(25):2.7 最大面积是多少(解析版)
题型:解答题
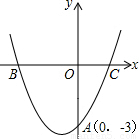
二次函数y=ax
2+bx+c的图象与x轴交于B、C两点,与y轴交于A点.
(1)根据图象确定a、b、c的符号,并说明理由;
(2)如果点A的坐标为(0,-3),∠ABC=45°,∠ACB=60°,求这个二次函数的解析式.
查看答案和解析>>
科目:
来源:第2章《二次函数》常考题集(25):2.7 最大面积是多少(解析版)
题型:解答题
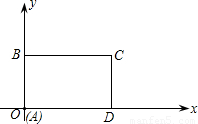
如图所示,在直角坐标系中,矩形ABCD的边AD在x轴上,点A在原点,AB=3,AD=5.若矩形以每秒2个单位长度沿x轴正方向作匀速运动.同时点P从A点出发以每秒1个单位长度沿A-B-C-D的路线作匀速运动.当P点运动到D点时停止运动,矩形ABCD也随之停止运动.
(1)求P点从A点运动到D点所需的时间;
(2)设P点运动时间为t(秒).
①当t=5时,求出点P的坐标;
②若△OAP的面积为s,试求出s与t之间的函数关系式(并写出相应的自变量t的取值范围).
查看答案和解析>>
科目:
来源:第2章《二次函数》常考题集(25):2.7 最大面积是多少(解析版)
题型:解答题
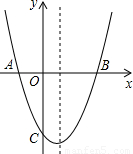
如图,抛物线y=x
2+bx+c与x轴交于A(-1,0),B(3,0)两点.
(1)求该抛物线的解析式;
(2)设(1)题中的抛物线上有一个动点P,当点P在抛物线上滑动到什么位置时,满足S
△PAB=8,并求出此时P点的坐标;
(3)设(1)题中的抛物线交y轴于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:
来源:第2章《二次函数》常考题集(25):2.7 最大面积是多少(解析版)
题型:解答题
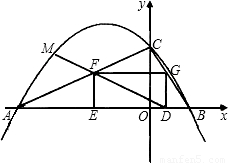
如图,抛物线y=ax
2+bx+c与x轴交于点A、B,与y轴交于点C,OC=4,AO=2OC,且抛物线对称轴为直线x=-3.
(1)求该抛物线的函数表达式;
(2)己知矩形DEFG的一条边DE在线段AB上,顶点F、G分别在AC、BC上,设OD=m,矩形DEFG的面积为S,当矩形DEFG的面积S取最大值时,连接DF并延长至点M,使
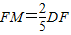
,求出此时点M的坐标;
(3)若点Q是抛物线上一点,且横坐标为-4,点P是y轴上一点,是否存在这样的点P,使得△BPQ是直角三角形?如果存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:
来源:第2章《二次函数》常考题集(25):2.7 最大面积是多少(解析版)
题型:解答题
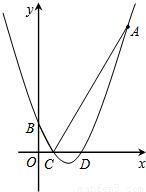
如图,抛物线的顶点坐标是
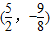
,且经过点A(8,14).
(1)求该抛物线的解析式;
(2)设该抛物线与y轴相交于点B,与x轴相交于C、D两点(点C在点D的左边),试求点B、C、D的坐标;
(3)设点P是x轴上的任意一点,分别连接AC、BC.试判断:PA+PB与AC+BC的大小关系,并说明理由.
查看答案和解析>>
科目:
来源:第2章《二次函数》常考题集(25):2.7 最大面积是多少(解析版)
题型:解答题
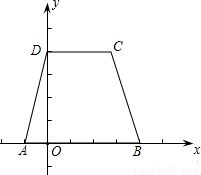
如图,在平面直角坐标系中,已知四边形ABCD是等腰梯形,A、B在x轴上,D在y轴上,AB∥CD,AD=BC=
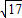
,AB=5,CD=3,抛物线y=-x
2+bx+c过A、B两点.
(1)求b、c;
(2)设M是x轴上方抛物线上的一动点,它到x轴与y轴的距离之和为d,求d的最大值;
(3)当(2)中M点运动到使d取最大值时,此时记点M为N,设线段AC与y轴交于点E,F为线段EC上一动点,求F到N点与到y轴的距离之和的最小值,并求此时F点的坐标.
查看答案和解析>>
科目:
来源:第2章《二次函数》常考题集(25):2.7 最大面积是多少(解析版)
题型:解答题
已知抛物线y=x2+(n-3)x+n+1经过坐标原点O.
(1)求这条抛物线的顶点P的坐标;
(2)设这条抛物线与x轴的另一个交点为A,求以直线PA为图象的一次函数解析式.
查看答案和解析>>
科目:
来源:第2章《二次函数》常考题集(25):2.7 最大面积是多少(解析版)
题型:解答题
如图,以矩形OCPD的顶点O为原点,它的两条边所在的直线分别为x轴和y轴建立直角坐标系.以点P为圆心,PC为半径的⊙P与x轴的正半轴交于A、B两点,若抛物线y=ax
2+bx+4经过A,B,C三点,且AB=6.
(1)求⊙P的半径R的长;
(2)求该抛物线的解析式并直接写出该抛物线与⊙P的第四个交点E的坐标;
(3)若以AB为直径的圆与直线AC的交点为F,求AF的长.

查看答案和解析>>
科目:
来源:第2章《二次函数》常考题集(25):2.7 最大面积是多少(解析版)
题型:解答题
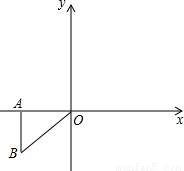
如图,△ABO中,O是坐标原点,A
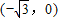
,B
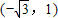
.
(1)①以原点O为位似中心,将△ABO放大,使变换后得到的△CDO与△ABO的位似比为2:1,且D在第一象限内,则C点坐标为(______
查看答案和解析>>
科目:
来源:第2章《二次函数》常考题集(25):2.7 最大面积是多少(解析版)
题型:解答题
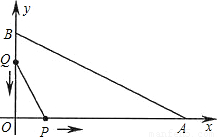
如图,在平面直角坐标系中,已知OA=12厘米,OB=6厘米.点P从点O开始沿OA边向点A以1厘米/秒的速度移动;点Q从点B开始沿BO边向点O以1厘米/秒的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6),那么
(1)设△POQ的面积为y,求y关于t的函数解析式;
(2)当△POQ的面积最大时,将△POQ沿直线PQ翻折后得到△PCQ,试判断点C是否落在直线AB上,并说明理由;
(3)当t为何值时,△POQ与△AOB相似.
查看答案和解析>>

 二次函数y=ax2+bx+c的图象与x轴交于B、C两点,与y轴交于A点.
二次函数y=ax2+bx+c的图象与x轴交于B、C两点,与y轴交于A点.

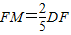 ,求出此时点M的坐标;
,求出此时点M的坐标;
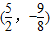 ,且经过点A(8,14).
,且经过点A(8,14).
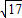 ,AB=5,CD=3,抛物线y=-x2+bx+c过A、B两点.
,AB=5,CD=3,抛物线y=-x2+bx+c过A、B两点.

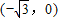 ,B
,B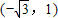 .
.
