相关习题
0 125540 125548 125554 125558 125564 125566 125570 125576 125578 125584 125590 125594 125596 125600 125606 125608 125614 125618 125620 125624 125626 125630 125632 125634 125635 125636 125638 125639 125640 125642 125644 125648 125650 125654 125656 125660 125666 125668 125674 125678 125680 125684 125690 125696 125698 125704 125708 125710 125716 125720 125726 125734 366461
科目：
来源：第2章《二次函数》常考题集（15）：2.6 何时获得最大利润（解析版）
题型：填空题
在平面直角坐标系中，点A、B、C的坐标分别为（0，1）、（4，2）、（2，6）．如果P（x，y）是△ABC围成的区域（含边界）上的点，那么当w=xy取得最大值时，点P的坐标是 ．
查看答案和解析>>
科目：
来源：第2章《二次函数》常考题集（15）：2.6 何时获得最大利润（解析版）
题型：填空题
在距离地面2m高的某处把一物体以初速度v
（m/s）竖直向上抛物出，在不计空气阻力的情况下，其上升高度s（m）与抛出时间t（s）满足：s=v
t-
gt
2（其中g是常数，通常取10m/s
2）．若v
=10m/s，则该物体在运动过程中最高点距地面
m．
查看答案和解析>>
科目：
来源：第2章《二次函数》常考题集（15）：2.6 何时获得最大利润（解析版）
题型：填空题
将进货单价为70元的某种商品按零售价100元售出时，每天能卖出20个．若这种商品的零售价在一定范围内每降价1元，其日销售量就增加了1个，为了获得最大利润，则应降价 元，最大利润为 元．
查看答案和解析>>
科目：
来源：第2章《二次函数》常考题集（15）：2.6 何时获得最大利润（解析版）
题型：填空题
某物体从上午7时至下午4时的温度M（℃）是时间t（小时）的函数：M=-2t2-5t+100（其中t=0表示中午12时，t=1表示下午1时），则上午10时此物体的温度为 ℃．
查看答案和解析>>
科目：
来源：第2章《二次函数》常考题集（15）：2.6 何时获得最大利润（解析版）
题型：解答题
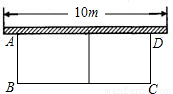
如图，有长为24米的篱笆，一面利用墙（墙的最大可用长度a为10米），围成中间隔有一道篱笆的长方形花圃．设花圃的宽AB为x米，面积为S米
2．
（1）求S与x的函数关系式；
（2）如果要围成面积为45米
2的花圃，AB的长是多少米？
（3）能围成面积比45米
2更大的花圃吗？如果能，请求出最大面积，并说明围法；如果不能，请说明理由．
查看答案和解析>>
科目：
来源：第2章《二次函数》常考题集（15）：2.6 何时获得最大利润（解析版）
题型：解答题
已知x1，x2是关于x的方程（x-2）（x-m）=（p-2）（p-m）的两个实数根．
（1）求x1，x2的值；
（2）若x1，x2是某直角三角形的两直角边的长，问当实数m，p满足什么条件时，此直角三角形的面积最大？并求出其最大值．
查看答案和解析>>
科目：
来源：第2章《二次函数》常考题集（15）：2.6 何时获得最大利润（解析版）
题型：解答题
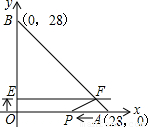
如图所示，已知A，B两点的坐标分别为（28，0）和（0，28）．动点P从A点开始在线段AO上以每秒3个单位的速度向原点O运动，动直线EF从x轴开始每秒1个单位的速度向上平行移动（即EF∥x轴），并且分别与y轴，线段AB交于E，F点，连接FP，设动点P与动直线EF同时出发，运动时间为t秒．
（1）当t=1秒时，求梯形OPFE的面积，当t为何值时，梯形OPFE的面积最大，最大面积是多少？
（2）当梯形OPFE的面积等于三角形APF的面积时，求线段PF的长；
（3）设t的值分别取t
1，t
2时（t
1≠t
2），所对应的三角形分别为△AF
1P
1和△AF
2P
2．试判断这两个三角形是否相似，请证明你的判断．
查看答案和解析>>
科目：
来源：第2章《二次函数》常考题集（15）：2.6 何时获得最大利润（解析版）
题型：解答题
一次函数y=x-3的图象与x轴，y轴分别交于点A，B．一个二次函数y=x2+bx+c的图象经过点A，B．
（1）求点A，B的坐标，并画出一次函数y=x-3的图象；
（2）求二次函数的解析式及它的最小值．
查看答案和解析>>
科目：
来源：第2章《二次函数》常考题集（15）：2.6 何时获得最大利润（解析版）
题型：解答题
已知二次函数y=x
2+bx+c中，函数y与自变量x的部分对应值如下表：
（1）求该二次函数的关系式；
（2）当x为何值时，y有最小值，最小值是多少？
（3）若A（m，y
1），B（m+1，y
2）两点都在该函数的图象上，试比较y
1与y
2的大小．
查看答案和解析>>
科目：
来源：第2章《二次函数》常考题集（15）：2.6 何时获得最大利润（解析版）
题型：解答题
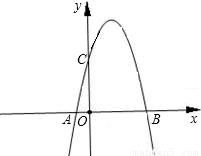
二次函数图象过A、C、B三点，点A的坐标为（-1，0），点B的坐标为（4，0），点C在y轴正半轴上，且AB=OC．
（1）求C的坐标；
（2）求二次函数的解析式，并求出函数最大值．
查看答案和解析>>
