相关习题
0 125593 125601 125607 125611 125617 125619 125623 125629 125631 125637 125643 125647 125649 125653 125659 125661 125667 125671 125673 125677 125679 125683 125685 125687 125688 125689 125691 125692 125693 125695 125697 125701 125703 125707 125709 125713 125719 125721 125727 125731 125733 125737 125743 125749 125751 125757 125761 125763 125769 125773 125779 125787 366461
科目:
来源:第2章《二次函数》中考题集(41):2.7 最大面积是多少(解析版)
题型:解答题
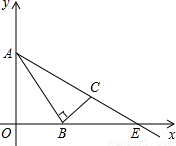
已知:如图,A(0,1)是y轴上一定点,B是x轴上一动点,以AB为边,在∠OAB的外部作∠BAE=∠OAB,过B作BC⊥AB,交AE于点C.
(1)当B点的横坐标为

时,求线段AC的长;
(2)当点B在x轴上运动时,设点C的纵、横坐标分别为y、x,试求y与x的函数关系式(当点B运动到O点时,点C也与O点重合);
(3)设过点P(0,-1)的直线l与(2)中所求函数的图象有两个公共点M
1(x
1,y
1)、M
2(x
2,y
2),且x
12+x
22-6(x
1+x
2)=8,求直线l的解析式.
查看答案和解析>>
科目:
来源:第2章《二次函数》中考题集(41):2.7 最大面积是多少(解析版)
题型:解答题
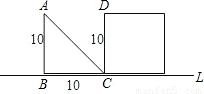
如图(单位:m),等腰三角形ABC以2米/秒的速度沿直线L向正方形移动,直到AB与CD重合.设x秒时,三角形与正方形重叠部分的面积为ym
2.
(1)写出y与x的关系式;
(2)当x=2,3.5时,y分别是多少?
(3)当重叠部分的面积是正方形面积的一半时,三角形移动了多长时间?
查看答案和解析>>
科目:
来源:第2章《二次函数》中考题集(41):2.7 最大面积是多少(解析版)
题型:解答题
已知抛物线y=ax
2+bx+c过点A(1,

),其顶点E的横坐标为2,此抛物线与x轴分别交于B(x
1,0),C(x
2,0)两点(x
1<x
2),且x
12+x
22=16.
(1)求此抛物线的解析式及顶点E的坐标;
(2)若D是y轴上一点,且△CDE为等腰三角形,求点D的坐标.
查看答案和解析>>
科目:
来源:第2章《二次函数》中考题集(41):2.7 最大面积是多少(解析版)
题型:解答题
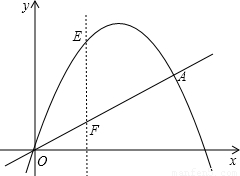
如图,已知二次函数y=-

x
2+4x+c的图象经过坐标原点,并且与函数y=

x的图象交于O、A两点.
(1)求c的值;
(2)求A点的坐标;
(3)若一条平行于y轴的直线与线段OA交于点F,与这个二次函数的图象交于点E,求线段EF的最大长度.
查看答案和解析>>
科目:
来源:第2章《二次函数》中考题集(41):2.7 最大面积是多少(解析版)
题型:解答题
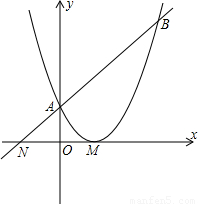
如图,已知二次函数y=

x
2+bx+c的图象与x轴只有一个公共点M,与y轴的交点为A,过点A的直线y=x+c与x轴交于点N,与这个二次函数的图象交于点B.
(1)求点A、B的坐标(用含b、c的式子表示);
(2)当S
△BMN=4S
△AMN时,求二次函数的解析式;
(3)在(2)的条件下,设点P为x轴上的一个动点,那么是否存在这样的点P,使得以P、A、M为顶点的三角形为等腰三角形?若存在,请写出符合条件的所有点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:
来源:第2章《二次函数》中考题集(41):2.7 最大面积是多少(解析版)
题型:解答题
已知:AC是⊙O的直径,点A、B、C、O在⊙O
1上,OA=2.建立如图所示的直角坐标系.∠ACO=∠ACB=60度.
(1)求点B关于x轴对称的点D的坐标;
(2)求经过三点A、B、O的二次函数的解析式;
(3)该抛物线上是否存在点P,使四边形PABO为梯形?若存在,请求出P点的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:
来源:第2章《二次函数》中考题集(41):2.7 最大面积是多少(解析版)
题型:解答题
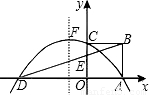
在如图所示的直角坐标系中,四边形OABC是边长为2的正方形,D为x轴上一点,连接BD交y轴于E点,且tan∠CBE=

.抛物线y=ax
2+bx+c(a≠0)过A、C、D三点,顶点为F.
(1)求D点坐标;
(2)求抛物线的解析式及顶点F的坐标;
(3)在直线DB上是否存在点P,使四边形PFDO为梯形?若存在,求出其坐标;若不存在,请说明理由.
查看答案和解析>>
科目:
来源:第2章《二次函数》中考题集(41):2.7 最大面积是多少(解析版)
题型:解答题
已知:如图,抛物线y=-

的图象与x轴分别交于A,B两点,与y轴交于C点,⊙M经过原点O及点A、C,点D是劣弧

上一动点(D点与A、O不重合).
(1)求抛物线的顶点E的坐标;
(2)求⊙M的面积;
(3)连CD交AO于点F,延长CD至G,使FG=2,试探究,当点D运动到何处时,直线GA与⊙M相切,并请说明理由.

查看答案和解析>>
科目:
来源:第2章《二次函数》中考题集(41):2.7 最大面积是多少(解析版)
题型:解答题
已知P(m,a)是抛物线y=ax
2上的点,且点P在第一象限.
(1)求m的值
(2)直线y=kx+b过点P,交x轴的正半轴于点A,交抛物线于另一点M.
①当b=2a时,∠OPA=90°是否成立?如果成立,请证明;如果不成立,举出一个反例说明;
②当b=4时,记△MOA的面积为S,求
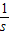
的最大值.
查看答案和解析>>
科目:
来源:第2章《二次函数》中考题集(41):2.7 最大面积是多少(解析版)
题型:解答题
如图1,连接△ABC的各边中点得到一个新的△A
1B
1C
1,又连接△A
1B
1C
1的各边中点得到△A
2B
2C
2,如此无限继续下去,得到一系列三角形:△ABC,△A
1B
1C
1,△A
2B
2C
2,…
已知A(0,0),B(3,0),C(2,2).

(1)求这一系列三角形趋向于一个点M的坐标;
(2)如图2,分别求出经过A,B,C三点的抛物线解析式和经过A
1,B
1,C
1三点的抛物线解析式;
(3)设两抛物线的交点分别为E、F,连接EF、EC
1、FC
1、EC
2、FC
2、C
1C
2,问:C
2与△EC
1F的关系是什么?
(4)如图3,问:A,A
2,C,C
2四点可不可能在同一条抛物线上,试说明理由.
查看答案和解析>>

 时,求线段AC的长;
时,求线段AC的长;

 ),其顶点E的横坐标为2,此抛物线与x轴分别交于B(x1,0),C(x2,0)两点(x1<x2),且x12+x22=16.
),其顶点E的横坐标为2,此抛物线与x轴分别交于B(x1,0),C(x2,0)两点(x1<x2),且x12+x22=16. x2+4x+c的图象经过坐标原点,并且与函数y=
x2+4x+c的图象经过坐标原点,并且与函数y= x的图象交于O、A两点.
x的图象交于O、A两点.
 x2+bx+c的图象与x轴只有一个公共点M,与y轴的交点为A,过点A的直线y=x+c与x轴交于点N,与这个二次函数的图象交于点B.
x2+bx+c的图象与x轴只有一个公共点M,与y轴的交点为A,过点A的直线y=x+c与x轴交于点N,与这个二次函数的图象交于点B.

 .抛物线y=ax2+bx+c(a≠0)过A、C、D三点,顶点为F.
.抛物线y=ax2+bx+c(a≠0)过A、C、D三点,顶点为F.
 的图象与x轴分别交于A,B两点,与y轴交于C点,⊙M经过原点O及点A、C,点D是劣弧
的图象与x轴分别交于A,B两点,与y轴交于C点,⊙M经过原点O及点A、C,点D是劣弧 上一动点(D点与A、O不重合).
上一动点(D点与A、O不重合).
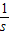 的最大值.
的最大值.