
科目: 来源:第2章《二次函数》中考题集(38):2.7 最大面积是多少(解析版) 题型:解答题
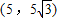 ,AB=10,点P从点A出发,沿A→B→C的方向匀速运动,同时点Q从点D(0,2)出发,沿y轴正方向以相同速度运动,当点P到达点C时,两点同时停止运动,设运动的时间为t秒.
,AB=10,点P从点A出发,沿A→B→C的方向匀速运动,同时点Q从点D(0,2)出发,沿y轴正方向以相同速度运动,当点P到达点C时,两点同时停止运动,设运动的时间为t秒.
查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(38):2.7 最大面积是多少(解析版) 题型:解答题
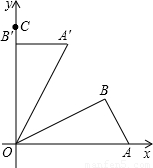
查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(38):2.7 最大面积是多少(解析版) 题型:解答题
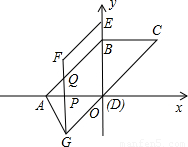
查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(38):2.7 最大面积是多少(解析版) 题型:解答题
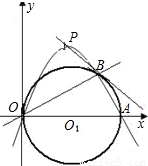
查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(38):2.7 最大面积是多少(解析版) 题型:解答题
查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(38):2.7 最大面积是多少(解析版) 题型:解答题
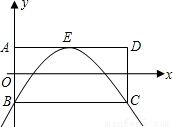
查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(38):2.7 最大面积是多少(解析版) 题型:解答题

查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(38):2.7 最大面积是多少(解析版) 题型:解答题
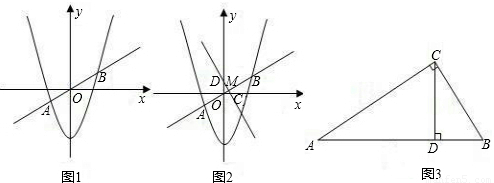
 与直线
与直线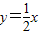 相交于A,B两点.
相交于A,B两点.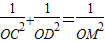 是否成立;
是否成立;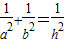 .
.
查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(38):2.7 最大面积是多少(解析版) 题型:解答题
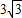 ).将△AOC绕AC的中点旋转180°,点O落到点B的位置,抛物线y=ax2-2
).将△AOC绕AC的中点旋转180°,点O落到点B的位置,抛物线y=ax2-2 x经过点A,点D是该抛物线的顶点.
x经过点A,点D是该抛物线的顶点.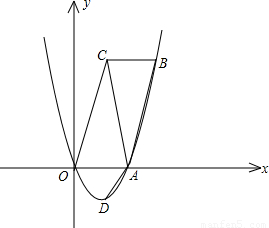
查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(38):2.7 最大面积是多少(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com