相关习题
0 125624 125632 125638 125642 125648 125650 125654 125660 125662 125668 125674 125678 125680 125684 125690 125692 125698 125702 125704 125708 125710 125714 125716 125718 125719 125720 125722 125723 125724 125726 125728 125732 125734 125738 125740 125744 125750 125752 125758 125762 125764 125768 125774 125780 125782 125788 125792 125794 125800 125804 125810 125818 366461
科目:
来源:第2章《二次函数》中考题集(27):2.7 最大面积是多少(解析版)
题型:解答题
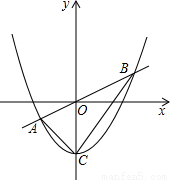
如图所示,已知直线y=

x与抛物线y=ax
2+b(a≠0)交于A(-4,-2),B(6,3)两点.抛物线与y轴的交点为C.
(1)求这个抛物线的解析式;
(2)在抛物线上存在点M,是△MAB是以AB为底边的等腰三角形,求点M的坐标;
(3)在抛物线上是否存在点P使得△PAC的面积是△ABC面积的

?若存在,试求出此时点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:
来源:第2章《二次函数》中考题集(27):2.7 最大面积是多少(解析版)
题型:解答题
如图1,抛物线
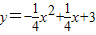
与x轴交于A、C两点,与y轴交于B点,与直线y=kx+b交于A、D两点.
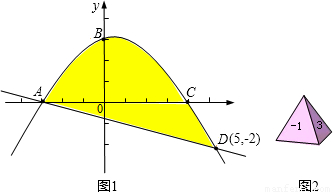
(1)直接写出A、C两点坐标和直线AD的解析式;
(2)如图2,质地均匀的正四面体骰子的各个面上依次标有数字-1、1、3、4.随机抛掷这枚骰子两次,把第一次着地一面的数字m记做P点的横坐标,第二次着地一面的数字n记做P点的纵坐标.则点P(m,n)落在图1中抛物线与直线围成区域内(图中阴影部分,含边界)的概率是多少?
查看答案和解析>>
科目:
来源:第2章《二次函数》中考题集(27):2.7 最大面积是多少(解析版)
题型:解答题
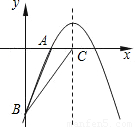
如图,已知二次函数y=-
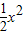
+bx+c的图象经过A(2,0)、B(0,-6)两点.
(1)求这个二次函数的解析式;
(2)设该二次函数的对称轴与x轴交于点C,连接BA、BC,求△ABC的面积.
查看答案和解析>>
科目:
来源:第2章《二次函数》中考题集(27):2.7 最大面积是多少(解析版)
题型:解答题
已知抛物线y=ax
2+bx+c经过A(-4,3)、B(2,0)两点,当x=3和x=-3时,这条抛物线上对应点的纵坐标相等.经过点C(0,-2)的直线l与x轴平行,O为坐标原点.
(1)求直线AB和这条抛物线的解析式;
(2)以A为圆心,AO为半径的圆记为⊙A,判断直线l与⊙A的位置关系,并说明理由;
(3)设直线AB上的点D的横坐标为-1,P(m,n)是抛物线y=ax
2+bx+c上的动点,当△PDO的周长最小时,求四边形CODP的面积.
查看答案和解析>>
科目:
来源:第2章《二次函数》中考题集(27):2.7 最大面积是多少(解析版)
题型:解答题
如图,已知点B(1,3),C(1,0),直线y=x+k经过点B,且与x轴交于点A,将△ABC沿直线AB折叠得到△ABD.
(1)填空:A点坐标为(______,______),D点坐标为(______,______);
(2)若抛物线y=

x
2+bx+c经过C,D两点,求抛物线的解析式;
(3)将(2)中的抛物线沿y轴向上平移,设平移后所得抛物线与y轴交点为E,点M是平移后的抛物线与直线AB的公共点,在抛物线平移过程中是否存在某一位置使得直线EM∥x轴.若存在,此时抛物线向上平移了几个单位?若不存在,请说明理由.
(提示:抛物线y=ax
2+bx+c(a≠0)的对称轴是x=-
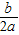
,顶点坐标是(-

,
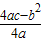
)

查看答案和解析>>
科目:
来源:第2章《二次函数》中考题集(27):2.7 最大面积是多少(解析版)
题型:解答题
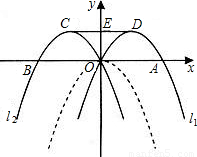
如图,把抛物线y=-x
2(虚线部分)向右平移1个单位长度,再向上平移1个单位长度,得出抛物线l
1,抛物线l
2与抛物线l
1关于y轴对称.点A,O,B分别是抛物线l
1,l
2与x轴的交点,D,C分别是抛物线l
1,l
2的顶点,线段CD交y轴于点E.
(1)分别写出抛物线l
1与l
2的解析式;
(2)设P使抛物线l
1上与D,O两点不重合的任意一点,Q点是P点关于y轴的对称点,试判断以P,Q,C,D为顶点的四边形是什么特殊的四边形?请说明理由.
(3)在抛物线l
1上是否存在点M,使得S
△ABM=S
四边形AOED?如果存在,求出M点的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:
来源:第2章《二次函数》中考题集(27):2.7 最大面积是多少(解析版)
题型:解答题
已知抛物线

上有不同的两点E(k+3,-k
2+1)和F(-k-1,-k
2+1).
(1)求抛物线的解析式;
(2)如图,抛物线

与x轴和y轴的正半轴分别交于点A和B,M为AB的中点,∠PMQ在AB的同侧以M为中心旋转,且∠PMQ=45°,MP交y轴于点C,MQ交x轴于点D.设AD的长为m(m>0),BC的长为n,求n和m之间的函数关系式;
(3)当m,n为何值时,∠PMQ的边过点F?

查看答案和解析>>
科目:
来源:第2章《二次函数》中考题集(27):2.7 最大面积是多少(解析版)
题型:解答题
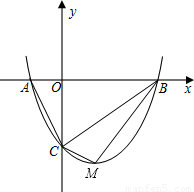
如图,抛物线y=mx
2-2mx-3m(m>0)与x轴交于A、B两点,与y轴交于C点.
(1)请求出抛物线顶点M的坐标(用含m的代数式表示),A、B两点的坐标;
(2)经探究可知,△BCM与△ABC的面积比不变,试求出这个比值;
(3)是否存在使△BCM为直角三角形的抛物线?若存在,请求出;如果不存在,请说明理由.
查看答案和解析>>
科目:
来源:第2章《二次函数》中考题集(27):2.7 最大面积是多少(解析版)
题型:解答题
如图,抛物线y=ax
2+bx+4与x轴的两个交点分别为A(-4,0)、B(2,0),与y轴交于点C,顶
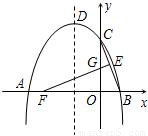
点为D.E(1,2)为线段BC的中点,BC的垂直平分线与x轴、y轴分别交于F、G.
(1)求抛物线的函数解析式,并写出顶点D的坐标;
(2)在直线EF上求一点H,使△CDH的周长最小,并求出最小周长;
(3)若点K在x轴上方的抛物线上运动,当K运动到什么位置时,△EFK的面积最大?并求出最大面积.
查看答案和解析>>
科目:
来源:第2章《二次函数》中考题集(27):2.7 最大面积是多少(解析版)
题型:解答题
如图,将腰长为

的等腰Rt△ABC(∠C是直角)放在平面直角坐标系中的第二象限,其中点A在y轴上,点B在抛物线y=ax
2+ax-2上,点C的坐标为(-1,0).
(1)点A的坐标为______,点B的坐标为______;
(2)抛物线的关系式为______,其顶点坐标为______;
(3)将三角板ABC绕顶点A逆时针方向旋转90°,到达△AB′C′的位置.请判断点B′、C′是否在(2)中的抛物线上,并说明理由.

查看答案和解析>>

 x与抛物线y=ax2+b(a≠0)交于A(-4,-2),B(6,3)两点.抛物线与y轴的交点为C.
x与抛物线y=ax2+b(a≠0)交于A(-4,-2),B(6,3)两点.抛物线与y轴的交点为C. ?若存在,试求出此时点P的坐标;若不存在,请说明理由.
?若存在,试求出此时点P的坐标;若不存在,请说明理由.
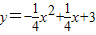 与x轴交于A、C两点,与y轴交于B点,与直线y=kx+b交于A、D两点.
与x轴交于A、C两点,与y轴交于B点,与直线y=kx+b交于A、D两点.
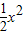 +bx+c的图象经过A(2,0)、B(0,-6)两点.
+bx+c的图象经过A(2,0)、B(0,-6)两点.
 x2+bx+c经过C,D两点,求抛物线的解析式;
x2+bx+c经过C,D两点,求抛物线的解析式;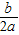 ,顶点坐标是(-
,顶点坐标是(- ,
,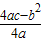 )
)

 上有不同的两点E(k+3,-k2+1)和F(-k-1,-k2+1).
上有不同的两点E(k+3,-k2+1)和F(-k-1,-k2+1). 与x轴和y轴的正半轴分别交于点A和B,M为AB的中点,∠PMQ在AB的同侧以M为中心旋转,且∠PMQ=45°,MP交y轴于点C,MQ交x轴于点D.设AD的长为m(m>0),BC的长为n,求n和m之间的函数关系式;
与x轴和y轴的正半轴分别交于点A和B,M为AB的中点,∠PMQ在AB的同侧以M为中心旋转,且∠PMQ=45°,MP交y轴于点C,MQ交x轴于点D.设AD的长为m(m>0),BC的长为n,求n和m之间的函数关系式;

 点为D.E(1,2)为线段BC的中点,BC的垂直平分线与x轴、y轴分别交于F、G.
点为D.E(1,2)为线段BC的中点,BC的垂直平分线与x轴、y轴分别交于F、G. 的等腰Rt△ABC(∠C是直角)放在平面直角坐标系中的第二象限,其中点A在y轴上,点B在抛物线y=ax2+ax-2上,点C的坐标为(-1,0).
的等腰Rt△ABC(∠C是直角)放在平面直角坐标系中的第二象限,其中点A在y轴上,点B在抛物线y=ax2+ax-2上,点C的坐标为(-1,0).