
科目: 来源:第2章《二次函数》中考题集(24):2.6 何时获得最大利润(解析版) 题型:解答题
 )2+
)2+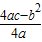 的形式,并据此说明:当x为何值时,租赁公司出租该型号设备的月收益最大?最大月收益是多少?
的形式,并据此说明:当x为何值时,租赁公司出租该型号设备的月收益最大?最大月收益是多少?查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(24):2.6 何时获得最大利润(解析版) 题型:解答题
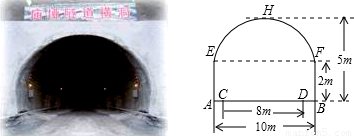
查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(24):2.6 何时获得最大利润(解析版) 题型:解答题
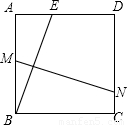
查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(24):2.6 何时获得最大利润(解析版) 题型:解答题
| 速度x (千米/时) | 5 | 10 | 15 | 20 | 25 | … | |
| 刹车距离y(米) |  | 2 | 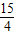 | 6 | 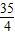 | … |
 x,请你就两车的速度方面分析相撞的原因.
x,请你就两车的速度方面分析相撞的原因.
查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(24):2.6 何时获得最大利润(解析版) 题型:解答题

查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(24):2.6 何时获得最大利润(解析版) 题型:解答题
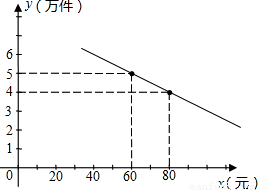
查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(24):2.6 何时获得最大利润(解析版) 题型:解答题
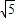 ≈2.24,
≈2.24,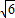 ≈2.45,计算结果保留两个有效数字.)
≈2.45,计算结果保留两个有效数字.)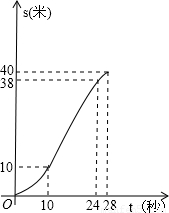
查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(24):2.6 何时获得最大利润(解析版) 题型:解答题
| 车站序号 | 在第x个车站起程时邮政车厢邮包总数 |
| 1 | n-1 |
| 2 | (n-1)-1+(n-2)=2(n-2) |
| 3 | 2(n-2)-2+(n-3)=3(n-3) |
| 4 | |
| 5 | |
| … | … |
| n |
查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(24):2.6 何时获得最大利润(解析版) 题型:解答题
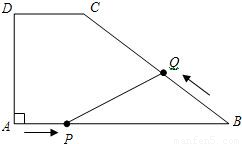
查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(24):2.6 何时获得最大利润(解析版) 题型:解答题
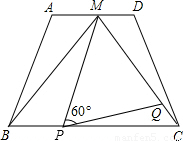
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com