
科目: 来源:第2章《二次函数》中考题集(23):2.6 何时获得最大利润(解析版) 题型:解答题

查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(23):2.6 何时获得最大利润(解析版) 题型:解答题

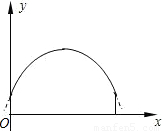
查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(23):2.6 何时获得最大利润(解析版) 题型:解答题
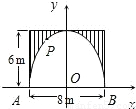
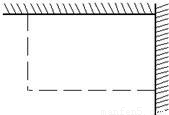 如图,用长为18 m的篱笆(虚线部分),两面靠墙围成矩形的苗圃.
如图,用长为18 m的篱笆(虚线部分),两面靠墙围成矩形的苗圃.查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(23):2.6 何时获得最大利润(解析版) 题型:解答题
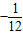 x2+
x2+ x+
x+
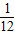 x2+
x2+ x+
x+ 化成y=a(x-h)2+k的形式.
化成y=a(x-h)2+k的形式.
查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(23):2.6 何时获得最大利润(解析版) 题型:解答题

查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(23):2.6 何时获得最大利润(解析版) 题型:解答题
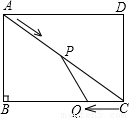
查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(23):2.6 何时获得最大利润(解析版) 题型:解答题
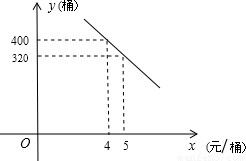
查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(23):2.6 何时获得最大利润(解析版) 题型:解答题
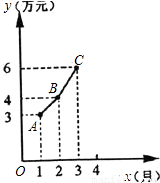 某公司2005年1-3月的月利润y(万元)与月份x之间的关系如图所示.图中的折线可近似看作是抛物线的一部分.
某公司2005年1-3月的月利润y(万元)与月份x之间的关系如图所示.图中的折线可近似看作是抛物线的一部分.查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(23):2.6 何时获得最大利润(解析版) 题型:解答题
查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(23):2.6 何时获得最大利润(解析版) 题型:解答题
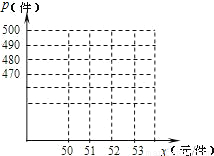
| 卖出价格x(元/件) | 50 | 51 | 52 | 53 | … |
| 销售量p(件) | 500 | 490 | 480 | 470 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com