
科目: 来源:第2章《二次函数》中考题集(17):2.6 何时获得最大利润(解析版) 题型:填空题
查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(17):2.6 何时获得最大利润(解析版) 题型:填空题
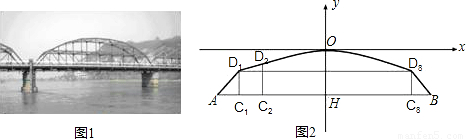
查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(17):2.6 何时获得最大利润(解析版) 题型:填空题
 x2,当涵洞水面宽AB为12米时,水面到桥拱顶点O的距离为 米.
x2,当涵洞水面宽AB为12米时,水面到桥拱顶点O的距离为 米.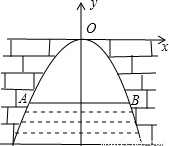
查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(17):2.6 何时获得最大利润(解析版) 题型:填空题
| 定价(元) | 100 | 110 | 120 | 130 | 140 | 150 |
| 销量(个) | 80 | 100 | 110 | 100 | 80 | 60 |
查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(17):2.6 何时获得最大利润(解析版) 题型:填空题
查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(17):2.6 何时获得最大利润(解析版) 题型:填空题
查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(17):2.6 何时获得最大利润(解析版) 题型:解答题
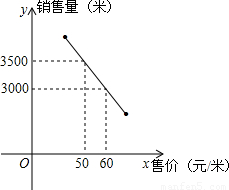
查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(17):2.6 何时获得最大利润(解析版) 题型:解答题
| 树苗 | 每棵树苗批发价格(元) | 两年后每棵树苗对空气的净化指数 |
| 杨树 | 3 | 0.4 |
| 丁香树 | 2 | 0.1 |
| 柳树 | p | 0.2 |
查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(17):2.6 何时获得最大利润(解析版) 题型:解答题
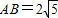 ,
,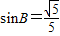 ,点P为边BC上一动点,PD∥AB,PD交AC于点D,连接AP.
,点P为边BC上一动点,PD∥AB,PD交AC于点D,连接AP.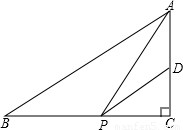
查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(17):2.6 何时获得最大利润(解析版) 题型:解答题
 cm/s的速度沿CB向终点B移动.过P作PE∥CB交AD于点E,设动点的运动时间为x秒.
cm/s的速度沿CB向终点B移动.过P作PE∥CB交AD于点E,设动点的运动时间为x秒.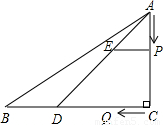
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com