相关习题
0 125656 125664 125670 125674 125680 125682 125686 125692 125694 125700 125706 125710 125712 125716 125722 125724 125730 125734 125736 125740 125742 125746 125748 125750 125751 125752 125754 125755 125756 125758 125760 125764 125766 125770 125772 125776 125782 125784 125790 125794 125796 125800 125806 125812 125814 125820 125824 125826 125832 125836 125842 125850 366461
科目:
来源:第2章《二次函数》中考题集(12):2.4 二次函数y=ax2+bx+c的图象(解析版)
题型:解答题
抛掷红、蓝两枚六面编号分别为1~6(整数)的质地均匀的正方体骰子,将红色和蓝色骰子正面朝上的编号分别作为二次函数y=x2+mx+n的一次项系数m和常数项n的值.
(1)问这样可以得到多少个不同形式的二次函数?(只需写出结果)
(2)请求出抛掷红、蓝骰子各一次,得到的二次函数图象顶点恰好在x轴上的概率是多少并说明理由.
查看答案和解析>>
科目:
来源:第2章《二次函数》中考题集(14):2.5 用三种方式表示二次函数(解析版)
题型:解答题
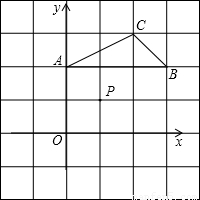
如图,在平面直角坐标系中,点A,B,C,P的坐标分别为(0,2),(3,2),(2,3),(1,1).
(1)请在图中画出△A′B′C′,使得△A′B′C′与△ABC关于点P成中心对称;
(2)若一个二次函数的图象经过(1)中△A′B′C′的三个顶点,求此二次函数的关系式.
查看答案和解析>>
科目:
来源:第2章《二次函数》中考题集(14):2.5 用三种方式表示二次函数(解析版)
题型:解答题
在平面直角坐标系中,有A(2,3)、B(3,2)两点.
(1)请再添加一点C,求出图象经过A、B、C三点的函数关系式.
(2)反思第(1)小问,考虑有没有更简捷的解题策略?请说出你的理由.
查看答案和解析>>
科目:
来源:第2章《二次函数》中考题集(14):2.5 用三种方式表示二次函数(解析版)
题型:解答题
已知二次函数y=ax
2+bx的图象经过点(2,0)、(-1,6)
(1)求二次函数的解析式;
(2)不用列表,在下图中画出函数图象,观察图象写出y>0时,x的取值范围.
查看答案和解析>>
科目:
来源:第2章《二次函数》中考题集(14):2.5 用三种方式表示二次函数(解析版)
题型:解答题
已知一抛物线与x轴的交点是A(-2,0)、B(1,0),且经过点C(2,8).
(1)求该抛物线的解析式;
(2)求该抛物线的顶点坐标.
查看答案和解析>>
科目:
来源:第2章《二次函数》中考题集(14):2.5 用三种方式表示二次函数(解析版)
题型:解答题
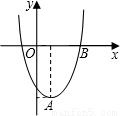
在直角坐标平面内,二次函数图象的顶点为A(1,-4),且过点B(3,0).
(1)求该二次函数的解析式;
(2)将该二次函数图象向右平移几个单位,可使平移后所得图象经过坐标原点?并直接写出平移后所得图象与x轴的另一个交点的坐标.
查看答案和解析>>
科目:
来源:第2章《二次函数》中考题集(14):2.5 用三种方式表示二次函数(解析版)
题型:解答题
已知二次函数图象的顶点是(-1,2),且过点
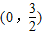
.
(1)求二次函数的表达式,并在图中画出它的图象;
(2)求证:对任意实数m,点M(m,-m
2)都不在这个二次函数的图象上.

查看答案和解析>>
科目:
来源:第2章《二次函数》中考题集(14):2.5 用三种方式表示二次函数(解析版)
题型:解答题
已知二次函数y=ax
2+bx+c(a≠0)的图象与y轴相交于点(0,-3),并经过点(-2,5),它的对称轴是x=1,如图为函数图象的一部分.
(1)求函数解析式,写出函数图象的顶点坐标;
(2)在原题图上,画出函数图象的其余部分;
(3)如果点P(n,-2n)在上述抛物线上,求n的值.
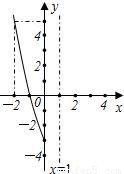
查看答案和解析>>
科目:
来源:第2章《二次函数》中考题集(14):2.5 用三种方式表示二次函数(解析版)
题型:解答题
已知抛物线y=ax
2+bx+c经过A,B,C三点,当x≥0时,其图象如图所示.
(1)求抛物线的解析式,写出抛物线的顶点坐标;
(2)画出抛物线y=ax
2+bx+c当x<0时的图象;
(3)利用抛物线y=ax
2+bx+c,写出x为何值时,y>0.
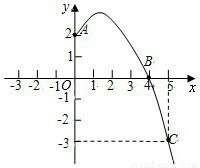
查看答案和解析>>
科目:
来源:第2章《二次函数》中考题集(14):2.5 用三种方式表示二次函数(解析版)
题型:解答题
已知二次函数图象经过(2,-3),对称轴x=1,抛物线与x轴两交点距离为4,求这个二次函数的解析式.
查看答案和解析>>



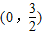 .
.

