相关习题
0 125703 125711 125717 125721 125727 125729 125733 125739 125741 125747 125753 125757 125759 125763 125769 125771 125777 125781 125783 125787 125789 125793 125795 125797 125798 125799 125801 125802 125803 125805 125807 125811 125813 125817 125819 125823 125829 125831 125837 125841 125843 125847 125853 125859 125861 125867 125871 125873 125879 125883 125889 125897 366461
科目:
来源:第1章《直角三角形的边角关系》常考题集(15):1.5 测量物体的高度(解析版)
题型:解答题
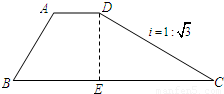
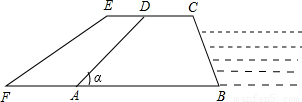
如图,梯形ABCD是拦水坝的横断面图,(图中i=1:
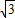
是指坡面的铅直高度DE与水平宽度CE的比),∠B=60°,AB=6,AD=4,求拦水坝的横断面ABCD的面积.(结果保留三位有效数字.参考数据:
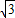
≈1.732,
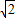
≈1.414)
查看答案和解析>>
科目:
来源:第1章《直角三角形的边角关系》常考题集(15):1.5 测量物体的高度(解析版)
题型:解答题
如图,某堤坝的横截面是梯形ABCD,背水坡AD的坡度i(即tanα)为1:1.2,坝高为5米,现为了提高堤坝的防洪抗洪能力,市防汛指挥部决定加固堤坝,要求坝顶CD加宽1米,形成新的背水坡EF,其坡度为1:1.4,已知堤坝总长度为4000米.
(1)求完成该工程需要多少土方?
(2)该工程由甲、乙两个工程队同时合作完成.按原计划需要20天.准备开工前接到上级通知,汛期可能提前,要求两个工程队提高工作效率,甲队工作效率提高30%,乙队工作效率提高40%,结果提前5天完成.问这两个工程队原计划每天各完成多少土方?
查看答案和解析>>
科目:
来源:第1章《直角三角形的边角关系》常考题集(15):1.5 测量物体的高度(解析版)
题型:解答题
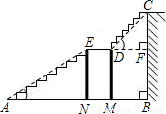
如图是某宾馆大厅到二楼的楼梯设计图,已知BC=6米,AB=9米,中间平台宽度DE为2米,DM,EN为平台的两根支柱,DM,EN垂直于AB,垂足分别为M,N,∠EAB=30°,∠CDF=45°.求DM和BC的水平距离BM.(精确到0.1米,参考数据:
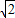
≈1.41,
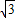
≈1.73)
查看答案和解析>>
科目:
来源:第1章《直角三角形的边角关系》常考题集(15):1.5 测量物体的高度(解析版)
题型:解答题
如图,某超市(大型商场)在一楼至二楼之间安装有电梯,天花板(一楼的楼顶墙壁)与地面平行,请你根据图中数据计算回答:小敏身高1.85米,他乘电梯会有碰头危险吗?(sin28°≈0.47,tan28°≈0.53)
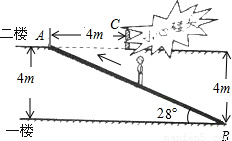
查看答案和解析>>
科目:
来源:第1章《直角三角形的边角关系》常考题集(18):1.5 测量物体的高度(解析版)
题型:解答题
如图,某一时刻太阳光从教室窗户射入室内,与地面的夹角∠BPC为30°,窗户的一部分在教室地面所形成的影长PE为3.5米,窗户的高度AF为2.5米.求窗外遮阳蓬外端一点D到教室窗户上椽的距离AD.(结果精确0.1米)
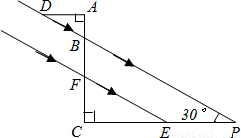
查看答案和解析>>
科目:
来源:第1章《直角三角形的边角关系》常考题集(18):1.5 测量物体的高度(解析版)
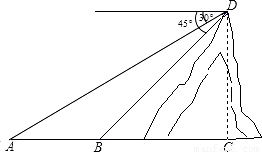
题型:解答题
某中学初三(2)班数学活动小组利用周日开展课外实践活动,他们要在湖面上测量建在地面上某塔AB的高度.如图,在湖面上点C测得塔顶A的仰角为45°,沿直线CD向塔AB方向前进18米到达点D,测得塔顶A的仰角为60度.已知湖面低于地平面1米,请你帮他们计算出塔AB的高度.(结果保留根号)
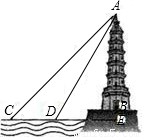
查看答案和解析>>
科目:
来源:第1章《直角三角形的边角关系》常考题集(18):1.5 测量物体的高度(解析版)
题型:解答题
如图,“五•一”期间在某商贸大厦上从点A到点B悬挂了一条宣传条幅,小明和小雯的家正好住在商贸大厦对面的家属楼上,小明在四楼D点测得条幅端点A的仰角为30°,测得条幅端点B的俯角为45°;小雯在三楼仰角为45°,测得条幅端点B的俯角为30°.若设楼层高度CD为3米,请你根据小明和小雯测得的数据求出条幅AB的长.
(结果精确到个位,参考数据

=1.73)

查看答案和解析>>
科目:
来源:第1章《直角三角形的边角关系》常考题集(18):1.5 测量物体的高度(解析版)
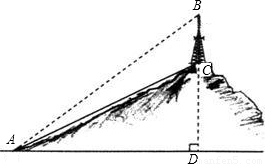
题型:解答题
如图,某人在山坡坡脚A处测得电视塔尖点C的仰角为60°,沿山坡向上走到P处再测得点C的仰角为45°,已知OA=100米,山坡坡度为

(即tan∠PAB=

),且O,A,B在同一条直线上.求电视塔OC的高度以及此人所在位置点P的铅直高度.(测倾器的高度忽略不计,结果保留根号形式)
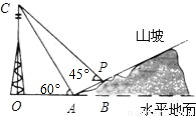
查看答案和解析>>
科目:
来源:第1章《直角三角形的边角关系》常考题集(18):1.5 测量物体的高度(解析版)
题型:解答题
如图,要测量小山上电视塔BC的高度,在山脚下点A测得:塔顶B的仰角为∠BAD=40°,塔底C的仰角为∠CAD=29°,AC=200米,求电视塔BC的高.(精确到1米)(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,sin29°≈0.48,cos29°≈0.87,tan29°≈0.55.)
查看答案和解析>>
科目:
来源:第1章《直角三角形的边角关系》常考题集(18):1.5 测量物体的高度(解析版)
题型:解答题
我边防战士在海拔高度(即CD的长)为50米的小岛顶部D处执行任务,上午8时发现在海面上的A处有一艘船,此时测得该船的俯角为30°,该船沿着AC方向一段时间后到达B处,又测得该船的俯角为45度.其该船在这一段时间内的航程?
(计算结果保留根号).
查看答案和解析>>

 是指坡面的铅直高度DE与水平宽度CE的比),∠B=60°,AB=6,AD=4,求拦水坝的横断面ABCD的面积.(结果保留三位有效数字.参考数据:
是指坡面的铅直高度DE与水平宽度CE的比),∠B=60°,AB=6,AD=4,求拦水坝的横断面ABCD的面积.(结果保留三位有效数字.参考数据: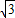 ≈1.732,
≈1.732,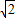 ≈1.414)
≈1.414)

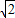 ≈1.41,
≈1.41,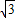 ≈1.73)
≈1.73)



 =1.73)
=1.73)
 (即tan∠PAB=
(即tan∠PAB= ),且O,A,B在同一条直线上.求电视塔OC的高度以及此人所在位置点P的铅直高度.(测倾器的高度忽略不计,结果保留根号形式)
),且O,A,B在同一条直线上.求电视塔OC的高度以及此人所在位置点P的铅直高度.(测倾器的高度忽略不计,结果保留根号形式)

