科目： 来源：第1章《直角三角形的边角关系》常考题集（10）：1.4 船有触角的危险吗（解析版） 题型：解答题

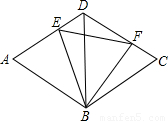
如图，菱形ABCD的边长为2，BD=2，E、F分别是边AD，CD上的两个动点，且满足AE+CF=2．
（1）求证：△BDE≌△BCF；
（2）判断△BEF的形状，并说明理由；
（3）设△BEF的面积为S，求S的取值范围．

科目： 来源：第1章《直角三角形的边角关系》常考题集（10）：1.4 船有触角的危险吗（解析版） 题型：解答题

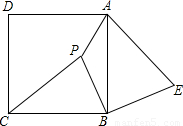
已知：如图，P是正方形ABCD内一点，在正方形ABCD外有一点E，满足∠ABE=∠CBP，BE=BP．
（1）求证：△CPB≌△AEB；
（2）求证：PB⊥BE；
（3）若PA：PB=1：2，∠APB=135°，求cos∠PAE的值．

科目： 来源：第1章《直角三角形的边角关系》常考题集（10）：1.4 船有触角的危险吗（解析版） 题型：解答题

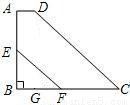
如图，在梯形ABCD中，AD∥BC，∠B=90°，∠C=45°，AD=1，BC=4，E为AB中点，EF∥DC交BC于点F，求EF的长．

科目： 来源：第1章《直角三角形的边角关系》常考题集（10）：1.4 船有触角的危险吗（解析版） 题型：解答题

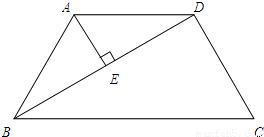
如图，在梯形ABCD中，AD∥BC，AB=DC=AD，∠C=60°，AE⊥BD于E，AE=1．求梯形ABCD的高．

科目： 来源：第1章《直角三角形的边角关系》常考题集（10）：1.4 船有触角的危险吗（解析版） 题型：解答题

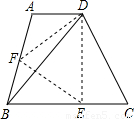
如图，等腰梯形ABCD中，AD∥BC，∠DBC=45°，翻折梯形ABCD，使点B与点D重合，折痕分别交边AB、BC于点F、E，若AD=2，BC=8．
（1）求BE的长；
（2）求∠CDE的正切值．

科目： 来源：第1章《直角三角形的边角关系》常考题集（10）：1.4 船有触角的危险吗（解析版） 题型：解答题

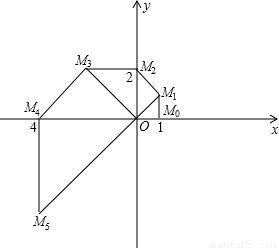
如图，在直角坐标系中，已知点M的坐标为（1，0），将线段OM绕原点O沿逆时针方向旋转45°，再将其延长到M₁，使得M₁M⊥OM，得到线段OM₁；又将线段OM₁绕原点O沿逆时针方向旋转45°，再将其延长到M₂，使得M₂M₁⊥OM₁，得到线段OM₂，如此下去，得到线段OM₃，OM₄，…，OM_n
（1）写出点M₅的坐标；
（2）求△M₅OM₆的周长；
（3）我们规定：把点M_n（x_n，y_n）（n=0，1，2，3…）的横坐标x_n，纵坐标y_n都取绝对值后得到的新坐标（|x_n|，|y_n|）称之为点M_n的“绝对坐标”．根据图中点M_n的分布规律，请你猜想点M_n的“绝对坐标”，并写出来．

科目： 来源：第1章《直角三角形的边角关系》常考题集（10）：1.4 船有触角的危险吗（解析版） 题型：解答题

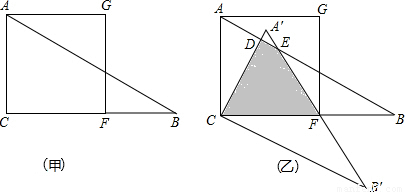
如图，把正方形ACFG与Rt△ACB按如图（甲）所示重叠在一起，其中AC=2，∠BAC=60°，若把Rt△ACB绕直角顶点C按顺时针方向旋转，使斜边AB恰好经过正方形ACFG的顶点F，得△A′B′C′，A B分别与A′C，A′B′相交于D、E，如图（乙）所示．
①△ACB至少旋转多少度才能得到△A′B′C′？说明理由；
②求△ACB与△A′B′C′的重叠部分（即四边形CDEF）的面积（若取近似值，则精确到0.1）？

科目： 来源：第1章《直角三角形的边角关系》常考题集（11）：1.4 船有触角的危险吗（解析版） 题型：解答题

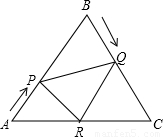
如图，已知△ABC是边长为6cm的等边三角形，动点P、Q同时从A、B两点出发，分别沿AB、BC匀速运动，其中点P运动的速度是1cm/s，点Q运动的速度是2cm/s，当点Q到达点C时，P、Q两点都停止运动，设运动时间为t（s），解答下列问题：
（1）当t=2时，判断△BPQ的形状，并说明理由；
（2）设△BPQ的面积为S（cm²），求S与t的函数关系式；
（3）作QR∥BA交AC于点R，连接PR，当t为何值时，△APR∽△PRQ．

科目： 来源：第1章《直角三角形的边角关系》常考题集（11）：1.4 船有触角的危险吗（解析版） 题型：解答题

将两块大小一样含30°角的直角三角板，叠放在一起，使得它们的斜边AB重合，直角边不重合，已知AB=8，BC=AD=4，AC与BD相交于点E，连接CD．

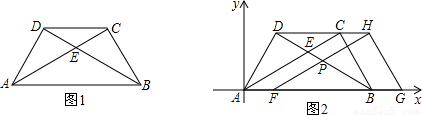
（1）填空：如图1，AC=______

科目： 来源：第1章《直角三角形的边角关系》常考题集（11）：1.4 船有触角的危险吗（解析版） 题型：解答题

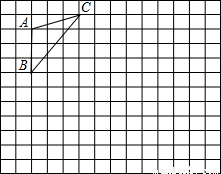
如图，方格纸上的每个小方格都是边长为1的正方形，我们把格点间连线为边的三角形称为“格点三角形”，图中的△ABC就是一个格点三角形．
（1）在△ABC中，BC=______，tanB=______；
（2）请在方格中画出一个格点三角形DEF，使△DEF∽△ABC，并且△DEF与△ABC的相似比为2．