相关习题
0 125719 125727 125733 125737 125743 125745 125749 125755 125757 125763 125769 125773 125775 125779 125785 125787 125793 125797 125799 125803 125805 125809 125811 125813 125814 125815 125817 125818 125819 125821 125823 125827 125829 125833 125835 125839 125845 125847 125853 125857 125859 125863 125869 125875 125877 125883 125887 125889 125895 125899 125905 125913 366461
科目:
来源:第1章《直角三角形的边角关系》常考题集(10):1.4 船有触角的危险吗(解析版)
题型:填空题
小明骑自行车以15千米/小时的速度在公路上向正北方向匀速行进,如图,出发时,在B点他观察到仓库A在他的北偏东30°处,骑行20分钟后到达C点,发现此时这座仓库正好在他的东南方向,则这座仓库到公路的距离为
千米.(参考数据:

≈1.732,结果保留两位有效数字)
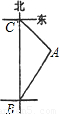
查看答案和解析>>
科目:
来源:第1章《直角三角形的边角关系》常考题集(10):1.4 船有触角的危险吗(解析版)
题型:填空题
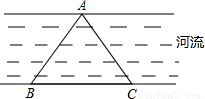
如图,B、C是洲河岸边两点,A是河对岸岸边一点,测得∠ABC=45°,∠ACB=45°,BC=200米,则点A到岸边BC的距离是
米.
查看答案和解析>>
科目:
来源:第1章《直角三角形的边角关系》常考题集(10):1.4 船有触角的危险吗(解析版)
题型:填空题
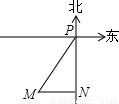
如图,一艘轮船向正东方向航行,上午9时测得它在灯塔P的南偏西30°方向、距离灯塔120海里的M处,上午11时到达这座灯塔的正南方向的N处,则这艘轮船在这段时间内航行的平均速度是
海里/小时.
查看答案和解析>>
科目:
来源:第1章《直角三角形的边角关系》常考题集(10):1.4 船有触角的危险吗(解析版)
题型:填空题
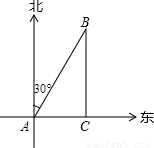
一轮船以每小时20海里的速度沿正东方向航行,上午8时,该船在A处测得某灯塔位于它的北偏东30°的B处,如图所示,上午9时行至C处,测得灯塔恰好在它的正北方向,此时它与灯塔的距离是
海里(结果保留根号).
查看答案和解析>>
科目:
来源:第1章《直角三角形的边角关系》常考题集(10):1.4 船有触角的危险吗(解析版)
题型:填空题
如图,为了求出湖两岸A、B两点之间的距离,观测者在湖边找到一点C,并分别测∠BAC=90°,∠ABC=30°,又量得BC=160m,则A、B两点之间距离为
m(结果保留根号).

查看答案和解析>>
科目:
来源:第1章《直角三角形的边角关系》常考题集(10):1.4 船有触角的危险吗(解析版)
题型:解答题
如图,在平面直角坐标系中,点A在第一象限,点B的坐标为(3,0),OA=2,∠AOB=60°.
(1)求点A的坐标;
(2)若直线AB交y轴于点C,求△AOC的面积.

查看答案和解析>>
科目:
来源:第1章《直角三角形的边角关系》常考题集(10):1.4 船有触角的危险吗(解析版)
题型:解答题
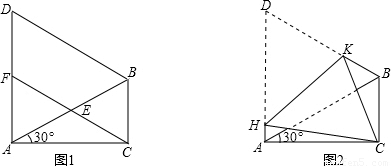
如图1,在△ABC中,∠ACB=90°,∠CAB=30°,△ABD是等边三角形,E是AB的中点,连接CE并延长交AD于F.
(1)求证:①△AEF≌△BEC;②四边形BCFD是平行四边形;
(2)如图2,将四边形ACBD折叠,使D与C重合,HK为折痕,求sin∠ACH的值.
查看答案和解析>>
科目:
来源:第1章《直角三角形的边角关系》常考题集(10):1.4 船有触角的危险吗(解析版)
题型:解答题
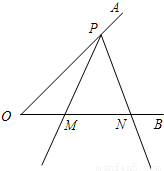
如图,已知P为∠AOB的边OA上的一点,以P为顶点的∠MPN的两边分别交射线OB于M、N两点,且∠MPN=∠AOB=α(α为锐角).当∠MPN以点P为旋转中心,PM边与PO重合的位置开始,按逆时针方向旋转(∠MPN保持不变)时,M、N两点在射线OB上同时以不同的速度向右平行移动.设OM=x,ON=y(y>x>0),△POM的面积为S.若sinα=
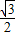
,OP=2.
(1)当∠MPN旋转30°(即∠OPM=30°)时,求点N移动的距离;
(2)求证:△OPN∽△PMN;
(3)写出y与x之间的关系式;
(4)试写出S随x变化的函数关系式,并确定S的取值范围.
查看答案和解析>>
科目:
来源:第1章《直角三角形的边角关系》常考题集(10):1.4 船有触角的危险吗(解析版)
题型:解答题
在边长为6的菱形ABCD中,动点M从点A出发,沿A?B?C向终点C运动,连接DM交AC于点N.
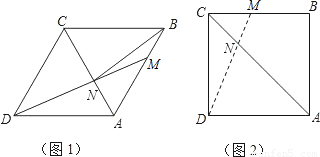
(1)如图1,当点M在AB边上时,连接BN:
①求证:△ABN≌△ADN;
②若∠ABC=60°,AM=4,∠ABN=α,求点M到AD的距离及tanα的值.
(2)如图2,若∠ABC=90°,记点M运动所经过的路程为x(6≤x≤12).试问:x为何值时,△ADN为等腰三角形.
查看答案和解析>>
科目:
来源:第1章《直角三角形的边角关系》常考题集(10):1.4 船有触角的危险吗(解析版)
题型:解答题
学校植物园沿路护栏纹饰部分设计成若干个全等菱形图案,每增加一个菱形图案,纹饰长度就增加dcm,如图所示.已知每个菱形图案的边长
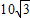
cm,其一个内角为60度.
(1)若d=26,则该纹饰要231个菱形图案,求纹饰的长度L;
(2)当d=20时,若保持(1)中纹饰长度不变,则需要多少个这样的菱形图案?

查看答案和解析>>

 ≈1.732,结果保留两位有效数字)
≈1.732,结果保留两位有效数字)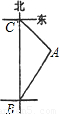






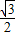 ,OP=2.
,OP=2.

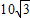 cm,其一个内角为60度.
cm,其一个内角为60度.