相关习题
0 125778 125786 125792 125796 125802 125804 125808 125814 125816 125822 125828 125832 125834 125838 125844 125846 125852 125856 125858 125862 125864 125868 125870 125872 125873 125874 125876 125877 125878 125880 125882 125886 125888 125892 125894 125898 125904 125906 125912 125916 125918 125922 125928 125934 125936 125942 125946 125948 125954 125958 125964 125972 366461
科目:
来源:第1章《直角三角形的边角关系》中考题集(24):1.4 船有触角的危险吗(解析版)
题型:解答题
如图所示,小明在公司里放风筝,拿风筝线的手B离地面高度AB为1.5米,风筝飞到C处时的线长BC为30米,这时测得∠CBD=60°,求此时风筝离地面的高度.(结果精确到0.1米,
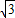
=1.73)
查看答案和解析>>
科目:
来源:第1章《直角三角形的边角关系》中考题集(24):1.4 船有触角的危险吗(解析版)
题型:解答题
在玉溪州大河旁边的路灯杆顶上有一个物体,它的抽象几何图形如图,若AB=4,AC=10,∠ABC=60°,求B、C两点间的距离.


查看答案和解析>>
科目:
来源:第1章《直角三角形的边角关系》中考题集(24):1.4 船有触角的危险吗(解析版)
题型:解答题
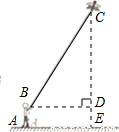
图1为已建设封项的16层楼房和其塔吊图,图2为其示意图,吊臂AB与地面EH平行,测得A点到楼顶D点的距离为5m,每层楼高3.5m,AE、BF、CH都垂直于地面,EF=16m,求塔吊的高CH的长?
查看答案和解析>>
科目:
来源:第1章《直角三角形的边角关系》中考题集(24):1.4 船有触角的危险吗(解析版)
题型:解答题
路边路灯的灯柱BC垂直于地面,灯杆BA的长为2米,灯杆与灯柱BC成120°角,锥形灯罩的轴线AD与灯杆AB垂直,且灯罩轴线AD正好通过道路路面的中心线(D在中心线上).已知点C与点D之间的距离为12米,求灯柱BC的高.(结果保留根号)

查看答案和解析>>
科目:
来源:第1章《直角三角形的边角关系》中考题集(24):1.4 船有触角的危险吗(解析版)
题型:解答题
如图,小明家所住楼房的高度AB=10米,到对面较高楼房的距离BD=20米,当阳光刚好从两楼房的顶部射入时,测得光线与水平线的夹角为40°.据此,小明便知楼房CD的高度.请你写出计算过程(结果精确到0.1米.参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)

查看答案和解析>>
科目:
来源:第1章《直角三角形的边角关系》中考题集(24):1.4 船有触角的危险吗(解析版)
题型:解答题
某课外活动小组测量学校旗杆的高度,当太阳光线与地面成35°角时,渢旗杆AB在地面上的投影BC的长为20米(如图).求旗杆AB的高度.(sin35°≈0.6,cos35°≈0.8,tan35°≈0.7)
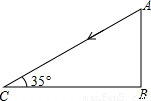
查看答案和解析>>
科目:
来源:第1章《直角三角形的边角关系》中考题集(24):1.4 船有触角的危险吗(解析版)
题型:解答题
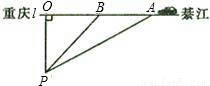
据交管部门统计,高速公路超速行驶是引发交通事故的主要原因.我县某校数学课外小组的几个同学想尝试用自己所学的知识检测车速,渝黔高速公路某路段的限速是:每小时80千米(即最高时速不超过80千米),如图,他们将观测点设在到公路l的距离为0.1千米的P处.这时,一辆轿车由綦江向重庆匀速直线驶来,测得此车从A处行驶到B处所用的时间为3秒(注:3秒=
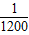
小时),并测得∠APO=59°,∠BPO=45°.试计算AB并判断此车是否超速?(精确到0.001).(参考数据:sin59°≈0.8572,cos59°≈0.5150,tan59°≈1.6643)
查看答案和解析>>
科目:
来源:第1章《直角三角形的边角关系》中考题集(24):1.4 船有触角的危险吗(解析版)
题型:解答题
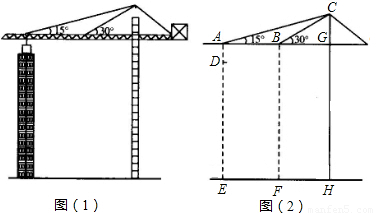
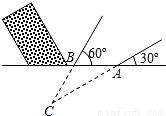
某地震救援队探测出某建筑物废墟下方点C处有生命迹象,已知废墟一侧地面上探测点A、B相距4m,探测线与地面的夹角分别是30°和60°,试确定生命所在点C的深度(结果精确到0.1m,参考数据:
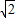
≈1.414,
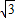
≈1.732)
查看答案和解析>>
科目:
来源:第1章《直角三角形的边角关系》中考题集(24):1.4 船有触角的危险吗(解析版)
题型:解答题
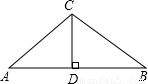
某厂房屋顶呈人字架形(等腰三角形),如图所示,已知AC=BC=8m,∠A=30°,CD⊥AB于点D.
(1)求∠ACB的大小;
(2)求AB的长度.
查看答案和解析>>
科目:
来源:第1章《直角三角形的边角关系》中考题集(24):1.4 船有触角的危险吗(解析版)
题型:解答题
如图,大海中有A和B两个岛屿,为测量它们之间的距离,在海岸线PQ上点E处测得∠AEP=74°,∠BEQ=30°;在点F处测得∠AFP=60°,∠BFQ=60°,EF=1km.
(1)判断AB,AE的数量关系,并说明理由;
(2)求两个岛屿A和B之间的距离(结果精确到0.1km).
(参考数据:
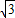
≈1.73,cos74°≈0.28,tan74°≈3.49,sin76°≈0.97,cos76°≈0.24)
查看答案和解析>>

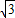 =1.73)
=1.73)






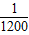 小时),并测得∠APO=59°,∠BPO=45°.试计算AB并判断此车是否超速?(精确到0.001).(参考数据:sin59°≈0.8572,cos59°≈0.5150,tan59°≈1.6643)
小时),并测得∠APO=59°,∠BPO=45°.试计算AB并判断此车是否超速?(精确到0.001).(参考数据:sin59°≈0.8572,cos59°≈0.5150,tan59°≈1.6643)
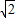 ≈1.414,
≈1.414,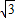 ≈1.732)
≈1.732)

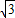 ≈1.73,cos74°≈0.28,tan74°≈3.49,sin76°≈0.97,cos76°≈0.24)
≈1.73,cos74°≈0.28,tan74°≈3.49,sin76°≈0.97,cos76°≈0.24)