
科目: 来源:第1章《直角三角形的边角关系》中考题集(22):1.4 船有触角的危险吗(解析版) 题型:解答题
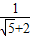 +(-3)
+(-3)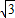 .求线段AD的长.
.求线段AD的长.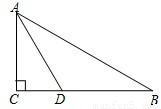
查看答案和解析>>
科目: 来源:第1章《直角三角形的边角关系》中考题集(22):1.4 船有触角的危险吗(解析版) 题型:解答题
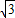 ,求AD的长.
,求AD的长.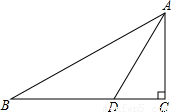
查看答案和解析>>
科目: 来源:第1章《直角三角形的边角关系》中考题集(22):1.4 船有触角的危险吗(解析版) 题型:解答题
 MD;
MD;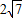 ,求tan∠ACP的值.
,求tan∠ACP的值.
查看答案和解析>>
科目: 来源:第1章《直角三角形的边角关系》中考题集(22):1.4 船有触角的危险吗(解析版) 题型:解答题
查看答案和解析>>
科目: 来源:第1章《直角三角形的边角关系》中考题集(22):1.4 船有触角的危险吗(解析版) 题型:解答题
 时,证明DC⊥OA;
时,证明DC⊥OA;
查看答案和解析>>
科目: 来源:第1章《直角三角形的边角关系》中考题集(22):1.4 船有触角的危险吗(解析版) 题型:解答题
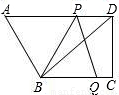
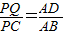 (如图1所示).
(如图1所示). ,且点Q在线段AB上时,设点B、Q之间的距离为x,
,且点Q在线段AB上时,设点B、Q之间的距离为x,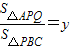 ,其中S△APQ表示△APQ的面积,S△PBC表示△PBC的面积,求y关于x的函数解析式,并写出函数定义域;
,其中S△APQ表示△APQ的面积,S△PBC表示△PBC的面积,求y关于x的函数解析式,并写出函数定义域;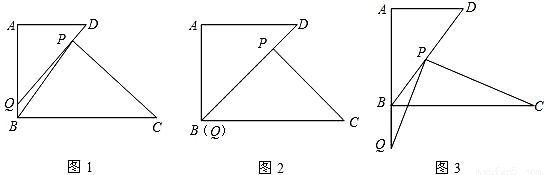
查看答案和解析>>
科目: 来源:第1章《直角三角形的边角关系》中考题集(22):1.4 船有触角的危险吗(解析版) 题型:解答题
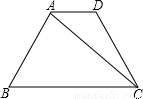
查看答案和解析>>
科目: 来源:第1章《直角三角形的边角关系》中考题集(22):1.4 船有触角的危险吗(解析版) 题型:解答题
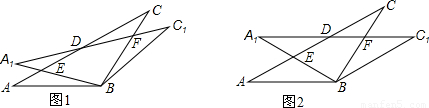
查看答案和解析>>
科目: 来源:第1章《直角三角形的边角关系》中考题集(22):1.4 船有触角的危险吗(解析版) 题型:解答题
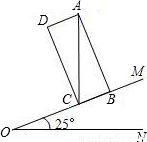
查看答案和解析>>
科目: 来源:第1章《直角三角形的边角关系》中考题集(23):1.4 船有触角的危险吗(解析版) 题型:解答题
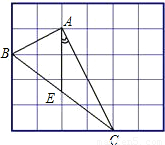
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com