
科目: 来源:第1章《直角三角形的边角关系》中考题集(22):1.4 船有触角的危险吗(解析版) 题型:解答题
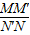 的值(用含α的三角函数表示).
的值(用含α的三角函数表示).
查看答案和解析>>
科目: 来源:第1章《直角三角形的边角关系》中考题集(22):1.4 船有触角的危险吗(解析版) 题型:解答题
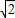 ,AB=
,AB=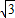 +1,则边BC的长为______.
+1,则边BC的长为______.查看答案和解析>>
科目: 来源:第1章《直角三角形的边角关系》中考题集(22):1.4 船有触角的危险吗(解析版) 题型:解答题
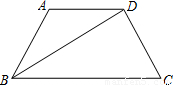
查看答案和解析>>
科目: 来源:第1章《直角三角形的边角关系》中考题集(22):1.4 船有触角的危险吗(解析版) 题型:解答题
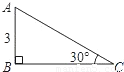
查看答案和解析>>
科目: 来源:第1章《直角三角形的边角关系》中考题集(22):1.4 船有触角的危险吗(解析版) 题型:解答题
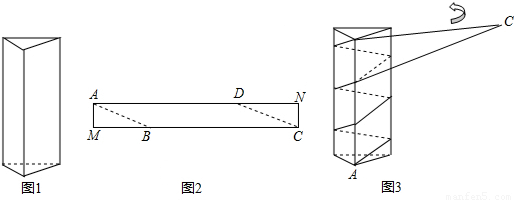
查看答案和解析>>
科目: 来源:第1章《直角三角形的边角关系》中考题集(22):1.4 船有触角的危险吗(解析版) 题型:解答题
 时,连接C′C,设四边形ACC′A′的面积为S,求S关于t的函数关系式;
时,连接C′C,设四边形ACC′A′的面积为S,求S关于t的函数关系式;
查看答案和解析>>
科目: 来源:第1章《直角三角形的边角关系》中考题集(22):1.4 船有触角的危险吗(解析版) 题型:解答题
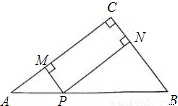
查看答案和解析>>
科目: 来源:第1章《直角三角形的边角关系》中考题集(22):1.4 船有触角的危险吗(解析版) 题型:解答题
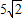 ,点E在AB上,∠AED=45°,DE=6,CE=7.求:AE的长及sin∠BCE的值.
,点E在AB上,∠AED=45°,DE=6,CE=7.求:AE的长及sin∠BCE的值.
查看答案和解析>>
科目: 来源:第1章《直角三角形的边角关系》中考题集(22):1.4 船有触角的危险吗(解析版) 题型:解答题
 时,求EF的长.
时,求EF的长.
查看答案和解析>>
科目: 来源:第1章《直角三角形的边角关系》中考题集(22):1.4 船有触角的危险吗(解析版) 题型:解答题
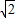 ,∠B=45°.动点M从B点出发沿线段BC以每秒2个单位长度的速度向终点C运动;动点N同时从C点出发沿线段CD以每秒1个单位长度的速度向终点D运动.设运动的时间为t秒.
,∠B=45°.动点M从B点出发沿线段BC以每秒2个单位长度的速度向终点C运动;动点N同时从C点出发沿线段CD以每秒1个单位长度的速度向终点D运动.设运动的时间为t秒.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com