
科目: 来源:第1章《直角三角形的边角关系》中考题集(04):1.1 从梯子的倾斜程度谈起(解析版) 题型:填空题
查看答案和解析>>
科目: 来源:第1章《直角三角形的边角关系》中考题集(04):1.1 从梯子的倾斜程度谈起(解析版) 题型:解答题
查看答案和解析>>
科目: 来源:第1章《直角三角形的边角关系》中考题集(04):1.1 从梯子的倾斜程度谈起(解析版) 题型:解答题
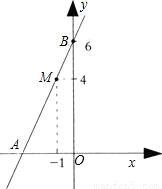
查看答案和解析>>
科目: 来源:第1章《直角三角形的边角关系》中考题集(04):1.1 从梯子的倾斜程度谈起(解析版) 题型:解答题
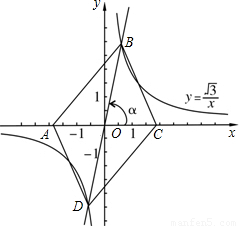 我们容易发现:反比例函数的图象是一个中心对称图形.你可以利用这一结论解决问题.如图,在同一直角坐标系中,正比例函数的图象可以看作是:将x轴所在的直线绕着原点O逆时针旋转α度角后的图形.若它与反比例函数
我们容易发现:反比例函数的图象是一个中心对称图形.你可以利用这一结论解决问题.如图,在同一直角坐标系中,正比例函数的图象可以看作是:将x轴所在的直线绕着原点O逆时针旋转α度角后的图形.若它与反比例函数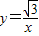 的图象分别交于第一、三象限的点B,D,已知点A(-m,O)、C(m,0).
的图象分别交于第一、三象限的点B,D,已知点A(-m,O)、C(m,0).查看答案和解析>>
科目: 来源:第1章《直角三角形的边角关系》中考题集(04):1.1 从梯子的倾斜程度谈起(解析版) 题型:解答题
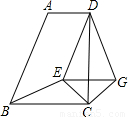
查看答案和解析>>
科目: 来源:第1章《直角三角形的边角关系》中考题集(04):1.1 从梯子的倾斜程度谈起(解析版) 题型:解答题
 ,求四边形PECF的面积.
,求四边形PECF的面积.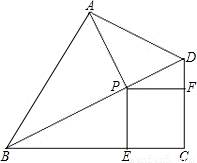
查看答案和解析>>
科目: 来源:第1章《直角三角形的边角关系》中考题集(04):1.1 从梯子的倾斜程度谈起(解析版) 题型:解答题
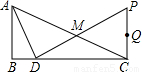
查看答案和解析>>
科目: 来源:第1章《直角三角形的边角关系》中考题集(04):1.1 从梯子的倾斜程度谈起(解析版) 题型:解答题
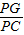 的值.
的值.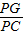 的值;
的值; 的值(用含α的式子表示).
的值(用含α的式子表示).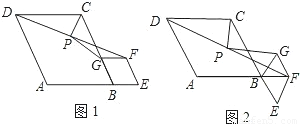
查看答案和解析>>
科目: 来源:第1章《直角三角形的边角关系》中考题集(04):1.1 从梯子的倾斜程度谈起(解析版) 题型:解答题
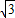 .
.
查看答案和解析>>
科目: 来源:第1章《直角三角形的边角关系》中考题集(04):1.1 从梯子的倾斜程度谈起(解析版) 题型:解答题
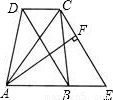
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com