
科目: 来源:第24章《圆(下)》中考题集(53):24.4 圆的有关计算(解析版) 题型:解答题
 的长为
的长为 ,求弦AD、AC的长.
,求弦AD、AC的长.
查看答案和解析>>
科目: 来源:第24章《圆(下)》中考题集(53):24.4 圆的有关计算(解析版) 题型:解答题
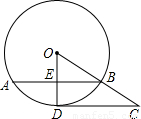
 .
.
查看答案和解析>>
科目: 来源:第24章《圆(下)》中考题集(53):24.4 圆的有关计算(解析版) 题型:解答题
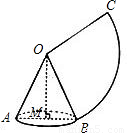
查看答案和解析>>
科目: 来源:第24章《圆(下)》中考题集(53):24.4 圆的有关计算(解析版) 题型:解答题
 的中点,AD⊥BC于点D,BP与AD相交于点E,若∠ACB=36°,BC=10.
的中点,AD⊥BC于点D,BP与AD相交于点E,若∠ACB=36°,BC=10. 的长;
的长;
查看答案和解析>>
科目: 来源:第24章《圆(下)》中考题集(53):24.4 圆的有关计算(解析版) 题型:解答题

查看答案和解析>>
科目: 来源:第24章《圆(下)》中考题集(53):24.4 圆的有关计算(解析版) 题型:解答题
 、
、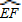 、
、 的圆心依次是A、B、C.
的圆心依次是A、B、C.
查看答案和解析>>
科目: 来源:第24章《圆(下)》中考题集(53):24.4 圆的有关计算(解析版) 题型:解答题
 ,BC=40cm,请你作出该小朋友将圆盘从A点滚动到D点其圆心所经过的路线的示意图,并求出此路线的长度.
,BC=40cm,请你作出该小朋友将圆盘从A点滚动到D点其圆心所经过的路线的示意图,并求出此路线的长度.查看答案和解析>>
科目: 来源:第24章《圆(下)》中考题集(53):24.4 圆的有关计算(解析版) 题型:解答题
 于E、F两点,若BC=2
于E、F两点,若BC=2 ,EF=1,求
,EF=1,求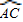 的长.
的长.
查看答案和解析>>
科目: 来源:第24章《圆(下)》中考题集(53):24.4 圆的有关计算(解析版) 题型:解答题
 线段DB,其中C,D在直线AB上.请你找出最短的行走路线,并求出这条路线的长度.(
线段DB,其中C,D在直线AB上.请你找出最短的行走路线,并求出这条路线的长度.( ≈1.73,π≈3.14)
≈1.73,π≈3.14)
查看答案和解析>>
科目: 来源:第24章《圆(下)》中考题集(53):24.4 圆的有关计算(解析版) 题型:解答题
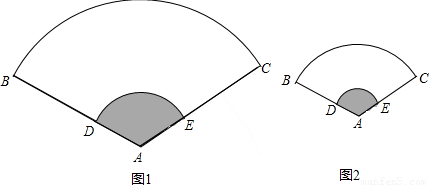
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com