相关习题
0 126131 126139 126145 126149 126155 126157 126161 126167 126169 126175 126181 126185 126187 126191 126197 126199 126205 126209 126211 126215 126217 126221 126223 126225 126226 126227 126229 126230 126231 126233 126235 126239 126241 126245 126247 126251 126257 126259 126265 126269 126271 126275 126281 126287 126289 126295 126299 126301 126307 126311 126317 126325 366461
科目:
来源:第24章《圆(下)》中考题集(23):24.2 圆的切线(解析版)
题型:解答题
如图,AB是⊙O的直径,点C在BA的延长线上,CA=AO,点D在⊙O上,∠ABD=30°.
(1)求证:CD是⊙O的切线;
(2)若点P在直线AB上,⊙P与⊙O外切于点B,与直线CD相切于点E,设⊙O与⊙P的半径分别为r与R,求
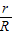
的值.
查看答案和解析>>
科目:
来源:第24章《圆(下)》中考题集(23):24.2 圆的切线(解析版)
题型:解答题
如图,已知AB为⊙O的直径,PA,PC是⊙O的切线,A,C为切点,∠BAC=30°.
(Ⅰ)求∠P的大小;
(Ⅱ)若AB=2,求PA的长(结果保留根号).

查看答案和解析>>
科目:
来源:第24章《圆(下)》中考题集(23):24.2 圆的切线(解析版)
题型:解答题
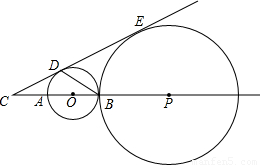
如图所示,在梯形ABCD中,AD∥BC,AB⊥BC,以AB为直径的⊙O与DC相切于E.已知AB=8,边BC比AD大6.
(1)求边AD、BC的长;
(2)在直径AB上是否存在一动点P,使以A、D、P为顶点的三角形与△BCP相似?若存在,求出AP的长;若不存在,请说明理由.
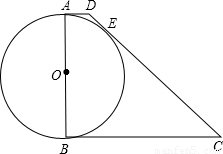
查看答案和解析>>
科目:
来源:第24章《圆(下)》中考题集(23):24.2 圆的切线(解析版)
题型:解答题
如图,Rt△BDE中,∠BDE=90°,BC平分∠DBE交DE于点C,AC⊥CB交BE于点A,△ABC的外接圆的半径为r.
(1)若∠E=30°,求证:BC•BD=r•ED;
(2)若BD=3,DE=4,求AE的长.
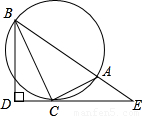
查看答案和解析>>
科目:
来源:第24章《圆(下)》中考题集(23):24.2 圆的切线(解析版)
题型:解答题
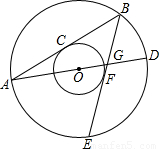
如图,两个同心圆的圆心是O,大圆的半径为13,小圆的半径为5,AD是大圆的直径.大圆的弦AB,BE分别与小圆相切于点C,F.AD,BE相交于点G,连接BD.
(1)求BD的长;
(2)求∠ABE+2∠D的度数;
(3)求
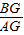
的值.
查看答案和解析>>
科目:
来源:第24章《圆(下)》中考题集(23):24.2 圆的切线(解析版)
题型:解答题
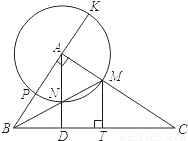
如图,在△ABC中,∠BAC=90度.BM平分∠ABC交AC于M,以A为圆心,AM为半径作⊙A交BM于N,AN的延长线交BC于D,直线AB交⊙A于P,K两点,作MT⊥BC于T.
(1)求证:AK=MT;
(2)求证:AD⊥BC;
(3)当AK=BD时,求证:
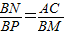
.
查看答案和解析>>
科目:
来源:第24章《圆(下)》中考题集(23):24.2 圆的切线(解析版)
题型:解答题
如图,△ABC内接于⊙O,过点B作⊙O的切线,交于CA的延长线于点E,∠EBC=2∠C.
(1)求证:AB=AC;
(2)当
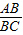
=
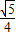
时,①求tan∠ABE的值;②如果AE=
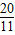
,求AC的值.

查看答案和解析>>
科目:
来源:第24章《圆(下)》中考题集(23):24.2 圆的切线(解析版)
题型:解答题
如图,某建筑工地上一钢管的横截面是圆环形.王师傅将直尺边缘紧靠内圆,直尺与外圆交于点A,B(AB与内圆相切于点C,其中点A在直尺的零刻度处).请观察图形,写出线段AB的长(精确到1cm),并根据得到的数据计算该钢管的横截面积.(结果用含π的式子表示)

查看答案和解析>>
科目:
来源:第24章《圆(下)》中考题集(23):24.2 圆的切线(解析版)
题型:解答题
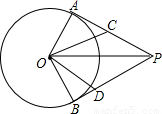
已知:如图,PA、PB是⊙O的切线;A、B是切点;连接OA、OB、OP,
(1)若∠AOP=60°,求∠OPB的度数;
(2)过O作OC、OD分别交AP、BP于C、D两点,
①若∠COP=∠DOP,求证:AC=BD;
②连接CD,设△PCD的周长为l,若l=2AP,判断直线CD与⊙O的位置关系,并说明理由.
查看答案和解析>>
科目:
来源:第24章《圆(下)》中考题集(23):24.2 圆的切线(解析版)
题型:解答题
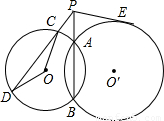
如图,⊙O和⊙O′都经过点A、B,点P在BA延长线上,过P作⊙O的割线PCD交⊙O于C、D两点,作⊙O′的切线PE切⊙O′于点E.若PC=4,CD=8,⊙O的半径为5.
(1)求PE的长;
(2)求△COD的面积.
查看答案和解析>>

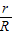 的值.
的值.



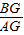 的值.
的值.
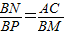 .
.
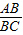 =
=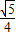 时,①求tan∠ABE的值;②如果AE=
时,①求tan∠ABE的值;②如果AE=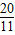 ,求AC的值.
,求AC的值.


