相关习题
0 126140 126148 126154 126158 126164 126166 126170 126176 126178 126184 126190 126194 126196 126200 126206 126208 126214 126218 126220 126224 126226 126230 126232 126234 126235 126236 126238 126239 126240 126242 126244 126248 126250 126254 126256 126260 126266 126268 126274 126278 126280 126284 126290 126296 126298 126304 126308 126310 126316 126320 126326 126334 366461
科目:
来源:第24章《圆(下)》中考题集(19):24.2 圆的切线(解析版)
题型:解答题
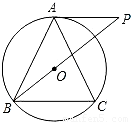
如图,圆O是△ABC的外接圆,AB=AC,过点A作AP∥BC,交BO的延长线于点P.
(1)求证:AP是圆O的切线;
(2)若圆O的半径R=5,BC=8,求线段AP的长.
查看答案和解析>>
科目:
来源:第24章《圆(下)》中考题集(19):24.2 圆的切线(解析版)
题型:解答题
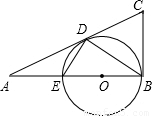
已知:如图,在Rt△ABC中,∠ABC=90°,以AB上的点O为圆心,OB的长为半径的圆与AB交于点E,与AC切于点D.
(1)求证:BC=CD;
(2)求证:∠ADE=∠ABD;
(3)设AD=2,AE=1,求⊙O直径的长.
查看答案和解析>>
科目:
来源:第24章《圆(下)》中考题集(19):24.2 圆的切线(解析版)
题型:解答题
如图,△ABC为等腰三角形,AB=AC,O是底边BC的中点,⊙O与腰AB相切于点D,求证:AC与⊙O相切.

查看答案和解析>>
科目:
来源:第24章《圆(下)》中考题集(19):24.2 圆的切线(解析版)
题型:解答题
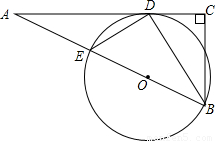
如图所示,在Rt△ABC中,∠C=90°,BC=3,CA=4,∠ABC的角平分线BD交AC于点D,点E是线段AB上的一点,以BE为直径的圆O过点D.
(1)求证:AC是圆O的切线;
(2)求AE的长.
查看答案和解析>>
科目:
来源:第24章《圆(下)》中考题集(19):24.2 圆的切线(解析版)
题型:解答题
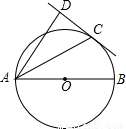
如图,已知AB是⊙O的直径,弦AC平分∠DAB,CD⊥AD于D.则CD是⊙O的切线吗?请说明理由.
查看答案和解析>>
科目:
来源:第24章《圆(下)》中考题集(19):24.2 圆的切线(解析版)
题型:解答题
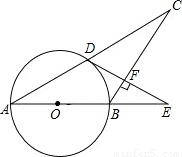
如图,在△ABC中,AB=BC,以AB为直径的⊙O与AC交于点D,过D作DF⊥BC,交AB的延长线于E,垂足为F.
(1)求证:直线DE是⊙O的切线;
(2)当AB=5,AC=8时,求cos∠E的值.
查看答案和解析>>
科目:
来源:第24章《圆(下)》中考题集(19):24.2 圆的切线(解析版)
题型:解答题
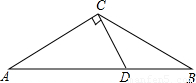
如图,已知在等腰△ABC中,∠A=∠B=30°,过点C作CD⊥AC交AB于点D.
(1)尺规作图:过A,D,C三点作⊙O(只要求作出图形,保留痕迹,不要求写作法);
(2)求证:BC是过A,D,C三点的圆的切线;
(3)若过A,D,C三点的圆的半径为
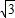
,则线段BC上是否存在一点P,使得以P,D,B为顶点的三角形与△BCO相似?若存在,求出DP的长;若不存在,请说明理由.
查看答案和解析>>
科目:
来源:第24章《圆(下)》中考题集(19):24.2 圆的切线(解析版)
题型:解答题
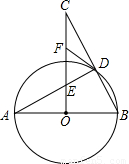
如图,AB为⊙O的直径,D是⊙O上的一点,过O点作AB的垂线交AD于点E,交BD的延长线于点C,F为CE上一点,且FD=FE.
(1)请探究FD与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为2,BD=
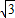
,求BC的长.
查看答案和解析>>
科目:
来源:第24章《圆(下)》中考题集(19):24.2 圆的切线(解析版)
题型:解答题
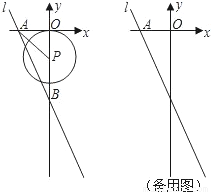
如图,在平面直角坐标系中,直线l:y=-2x-8分别与x轴,y轴相交于A,B两点,点P(0,k)是y轴的负半轴上的一个动点,以P为圆心,3为半径作⊙P.
(1)连接PA,若PA=PB,试判断⊙P与x轴的位置关系,并说明理由;
(2)当k为何值时,以⊙P与直线l的两个交点和圆心P为顶点的三角形是正三角形.
查看答案和解析>>
科目:
来源:第24章《圆(下)》中考题集(19):24.2 圆的切线(解析版)
题型:解答题
如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=12cm,AD=8cm,BC=22cm,AB为⊙O的直径,动点P从点A开始沿AD边向点D以1cm/s的速度运动,动点Q从点C开始沿CB边向点B以2cm/s的速度运动.P、Q分别从点A、C同时出发,当其中一个动点到
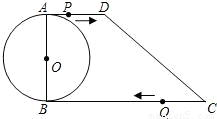
达端点时,另一个动点也随之停止运动,设运动时间为t(s).
(1)当t为何值时,四边形PQCD为平行四边形?
(2)当t为何值时,PQ与⊙O相切?
查看答案和解析>>







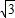 ,则线段BC上是否存在一点P,使得以P,D,B为顶点的三角形与△BCO相似?若存在,求出DP的长;若不存在,请说明理由.
,则线段BC上是否存在一点P,使得以P,D,B为顶点的三角形与△BCO相似?若存在,求出DP的长;若不存在,请说明理由.
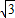 ,求BC的长.
,求BC的长.

 达端点时,另一个动点也随之停止运动,设运动时间为t(s).
达端点时,另一个动点也随之停止运动,设运动时间为t(s).