相关习题
0 126150 126158 126164 126168 126174 126176 126180 126186 126188 126194 126200 126204 126206 126210 126216 126218 126224 126228 126230 126234 126236 126240 126242 126244 126245 126246 126248 126249 126250 126252 126254 126258 126260 126264 126266 126270 126276 126278 126284 126288 126290 126294 126300 126306 126308 126314 126318 126320 126326 126330 126336 126344 366461
科目:
来源:第24章《圆(下)》中考题集(13):24.2 圆的切线(解析版)
题型:解答题
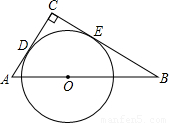
如图,在△ABC中,∠C=90°,AC+BC=8,点O是斜边AB上一点,以O为圆心的⊙O分别与AC,BC相切于点D,E.
(1)当AC=2时,求⊙O的半径;
(2)设AC=x,⊙O的半径为y,求y与x的函数关系式.
查看答案和解析>>
科目:
来源:第24章《圆(下)》中考题集(13):24.2 圆的切线(解析版)
题型:解答题
如图,⊙O是△ABC的外接圆,∠A=30°,AB是⊙O的直径,过点C作⊙O的切线,交AB延长线于D,CD=3
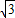
cm,
(1)求⊙O的直径;
(2)若动点M以3cm/s的速度从点A出发沿AB方向运动,同时点N以1.5cm/s的速度从B点出发沿BC方向运动.设运动的时间为t(0≤t≤2),连接MN,当t为何值时△BMN为直角三角形?并求此时该三角形的面积?
查看答案和解析>>
科目:
来源:第24章《圆(下)》中考题集(13):24.2 圆的切线(解析版)
题型:解答题
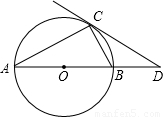
如图,AB是⊙O的直径,C为圆周上一点,∠ABC=30°,⊙O过点B的切线与CO的延长线交于点D.
求证:(1)∠CAB=∠BOD;
(2)△ABC≌△ODB.
查看答案和解析>>
科目:
来源:第24章《圆(下)》中考题集(13):24.2 圆的切线(解析版)
题型:解答题
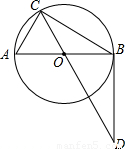
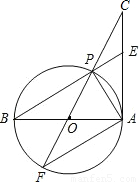
如图所示,AB是⊙O的直径,AC切⊙O于点A,且AC=AB,CO交⊙O于点P,CO的延长线交⊙O于点F,BP的延长线交AC于点E,连接AP、AF.
求证:
(1)AF∥BE;
(2)△ACP∽△FCA;
(3)CP=AE.
查看答案和解析>>
科目:
来源:第24章《圆(下)》中考题集(13):24.2 圆的切线(解析版)
题型:解答题
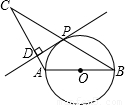
如图所示,在△ABC中,以AB为直径的⊙O交BC于点P,PD⊥AC于点D,且PD与⊙O相切.
(1)求证:AB=AC;
(2)若BC=6,AB=4,求CD的值.
查看答案和解析>>
科目:
来源:第24章《圆(下)》中考题集(13):24.2 圆的切线(解析版)
题型:解答题
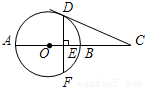
如图,AB是⊙O的直径,点C在AB的延长线上,CD切⊙O于点D,过点D作DF⊥AB于点E,交⊙O于点F,已知OE=1cm,DF=4cm.
(1)求⊙O的半径;
(2)求切线CD的长.
查看答案和解析>>
科目:
来源:第24章《圆(下)》中考题集(13):24.2 圆的切线(解析版)
题型:解答题
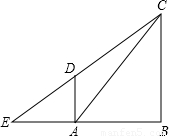
如图,已知Rt△ABC和Rt△EBC,∠B=90°.以边AC上的点O为圆心、OA为半径的⊙O与EC相切,D为切点,AD∥BC.
(1)用尺规确定并标出圆心O;(不写作法和证明,保留作图痕迹)
(2)求证:∠E=∠ACB;
(3)若AD=1,
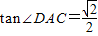
,求BC的长.
查看答案和解析>>
科目:
来源:第24章《圆(下)》中考题集(13):24.2 圆的切线(解析版)
题型:解答题
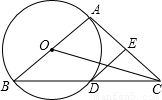
如图以△ABC的一边AB为直径作⊙O,⊙O与BC边的交点D恰好为BC的中点,过点D作⊙O的切线交AC边于点E.
(1)求证:DE⊥AC;
(2)若∠ABC=30°,求tan∠BCO的值.
查看答案和解析>>
科目:
来源:第24章《圆(下)》中考题集(13):24.2 圆的切线(解析版)
题型:解答题
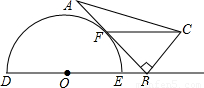
如图是一个量角器和一个含30°角的直角三角板放置在一起的示意图,其中点B在半圆O的直径DE的延长线上,AB切半圆O于点F,且BC=OE.
(1)求证:DE∥CF;
(2)当OE=2时,若以O,B,F为顶点的三角形与△ABC相似,求OB的长;
(3)若OE=2,移动三角板ABC且使AB边始终与半圆O相切,直角顶点B在直径DE的延长线上移动,求出点B移动的最大距离.
查看答案和解析>>
科目:
来源:第24章《圆(下)》中考题集(13):24.2 圆的切线(解析版)
题型:解答题
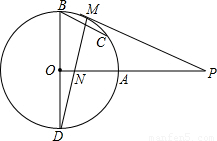
如图,BD是⊙O的直径,OA⊥OB,M是劣弧
上一点,过点M作⊙O的切线MP交OA的延长线于P点,MD与OA交于N点.
(1)求证:PM=PN;
(2)若BD=4,PA=

AO,过点B作BC∥MP交⊙O于C点,求BC的长.
查看答案和解析>>


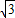 cm,
cm,




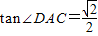 ,求BC的长.
,求BC的长.


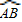 上一点,过点M作⊙O的切线MP交OA的延长线于P点,MD与OA交于N点.
上一点,过点M作⊙O的切线MP交OA的延长线于P点,MD与OA交于N点. AO,过点B作BC∥MP交⊙O于C点,求BC的长.
AO,过点B作BC∥MP交⊙O于C点,求BC的长.