相关习题
0 126153 126161 126167 126171 126177 126179 126183 126189 126191 126197 126203 126207 126209 126213 126219 126221 126227 126231 126233 126237 126239 126243 126245 126247 126248 126249 126251 126252 126253 126255 126257 126261 126263 126267 126269 126273 126279 126281 126287 126291 126293 126297 126303 126309 126311 126317 126321 126323 126329 126333 126339 126347 366461
科目:
来源:第24章《圆(下)》中考题集(12):24.2 圆的切线(解析版)
题型:解答题
如图,二次函数y=ax
2+bx+c(a>0)与坐标轴交于点A、B、C且OA=1,OB=OC=3.
(1)求此二次函数的解析式;
(2)写出顶点坐标和对称轴方程;
(3)点M、N在y=ax
2+bx+c的图象上(点N在点M的右边),且MN∥x轴,求以MN为直径且与x轴相切的圆的半径.

查看答案和解析>>
科目:
来源:第24章《圆(下)》中考题集(12):24.2 圆的切线(解析版)
题型:解答题
如图,点C是半圆O的半径OB上的动点,作PC⊥AB于C.点D是半圆上位于PC左侧的点,连接BD交线段PC于E,且PD=PE.
(1)求证:PD是⊙O的切线;
(2)若⊙O的半径为
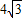
,PC=
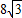
,设OC=x,PD
2=y.
①求y关于x的函数关系式;
②当
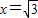
时,求tanB的值.
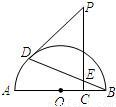
查看答案和解析>>
科目:
来源:第24章《圆(下)》中考题集(12):24.2 圆的切线(解析版)
题型:解答题
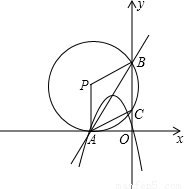
如图,在直角坐标系中,点A的坐标为(-2
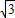
,0),⊙P刚好与x轴相切于点A,⊙P交y的正半轴于点B,点C,且BC=4.
(1)求半径PA的长;
(2)求证:四边形CAPB为菱形;
(3)有一开口向下的抛物线过O,A两点,当它的顶点不在直线AB的上方时,求函数表达式的二次项系数a的取值范围.
查看答案和解析>>
科目:
来源:第24章《圆(下)》中考题集(12):24.2 圆的切线(解析版)
题型:解答题
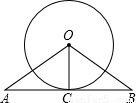
如图,等腰△OAB中,OA=OB,以点O为圆心作圆与底边AB相切于点C.
求证:AC=BC.
查看答案和解析>>
科目:
来源:第24章《圆(下)》中考题集(12):24.2 圆的切线(解析版)
题型:解答题
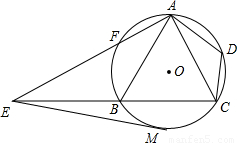
如图,已知四边形ABCD内接于⊙O,A是

的中点,AE⊥AC于A,与⊙O及CB的延长线分别交于点F、E,且
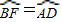
,EM切⊙O于M.
(1)求证:△ADC∽△EBA;
(2)求证:AC
2=

BC•CE;
(3)如果AB=2,EM=3,求cot∠CAD的值.
查看答案和解析>>
科目:
来源:第24章《圆(下)》中考题集(12):24.2 圆的切线(解析版)
题型:解答题
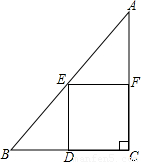
如图是某居民小区的一块直角三角形空地ABC,某斜边AB=100米,直角边AC=80米.现要利用这块空地建一个矩形停车场DCFE,使得D点在BC边上,E、F分别是AB、AC边的中点.
(1)求另一条直角边BC的长度;
(2)求停车场DCFE的面积;
(3)为了提高空地利用律,现要在剩余的△BDE中,建一个半圆形的花坛,使它的圆心在BE边上,且使花坛的面积达到最大,请你在原图中画出花坛的草图,求出它的半径(不要求说明面积最大的理由),并求此时直角三角形空地ABC的总利用率是百分之几(精确到1%).
查看答案和解析>>
科目:
来源:第24章《圆(下)》中考题集(12):24.2 圆的切线(解析版)
题型:解答题
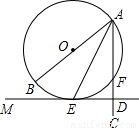
如图,AB是⊙O的直径,AE平分∠BAC交⊙O于点E,过E作⊙O的切线ME交AC于点D.试判断△AED的形状,并说明理由.
查看答案和解析>>
科目:
来源:第24章《圆(下)》中考题集(12):24.2 圆的切线(解析版)
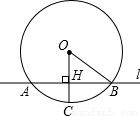
题型:解答题
如图,直线l与⊙O相交于A,B两点,且与半径OC垂直,垂足为H,已知AB=16cm,
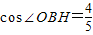
.
(1)求⊙O的半径;
(2)如果要将直线l向下平移到与⊙O相切的位置,平移的距离应是多少?请说明理由.
查看答案和解析>>
科目:
来源:第24章《圆(下)》中考题集(12):24.2 圆的切线(解析版)
题型:解答题
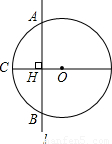
如图,⊙O的半径OC=10cm,直线l⊥CO,垂足为H,交⊙O于A,B两点,AB=16cm,直线l平移多少厘米时能与⊙O相切?
查看答案和解析>>
科目:
来源:第24章《圆(下)》中考题集(12):24.2 圆的切线(解析版)
题型:解答题
如图,AB是⊙O的切线,A为切点,AC是⊙O的弦,过O作OH⊥AC于点H.若OH=2,AB=12,BO=13.
求:(1)⊙O的半径;
(2)sin∠OAC的值;
(3)弦AC的长.(结果保留两个有效数字)

查看答案和解析>>


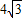 ,PC=
,PC=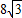 ,设OC=x,PD2=y.
,设OC=x,PD2=y.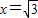 时,求tanB的值.
时,求tanB的值.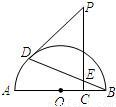
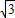 ,0),⊙P刚好与x轴相切于点A,⊙P交y的正半轴于点B,点C,且BC=4.
,0),⊙P刚好与x轴相切于点A,⊙P交y的正半轴于点B,点C,且BC=4.

 的中点,AE⊥AC于A,与⊙O及CB的延长线分别交于点F、E,且
的中点,AE⊥AC于A,与⊙O及CB的延长线分别交于点F、E,且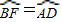 ,EM切⊙O于M.
,EM切⊙O于M. BC•CE;
BC•CE;


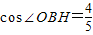 .
.

