相关习题
0 126353 126361 126367 126371 126377 126379 126383 126389 126391 126397 126403 126407 126409 126413 126419 126421 126427 126431 126433 126437 126439 126443 126445 126447 126448 126449 126451 126452 126453 126455 126457 126461 126463 126467 126469 126473 126479 126481 126487 126491 126493 126497 126503 126509 126511 126517 126521 126523 126529 126533 126539 126547 366461
科目:
来源:第35章《圆(二)》中考题集(13):35.3 探索切线的性质(解析版)
题型:解答题
如图,在△ABC中,∠C=90°,AC=3,BC=4.0为BC边上一点,以0为圆心,OB为半径作半圆与BC边和AB边分别交于点D、点E,连接DE.
(1)当BD=3时,求线段DE的长;
(2)过点E作半圆O的切线,当切线与AC边相交时,设交点为F.求证:△FAE是等腰三角形.

查看答案和解析>>
科目:
来源:第35章《圆(二)》中考题集(13):35.3 探索切线的性质(解析版)
题型:解答题
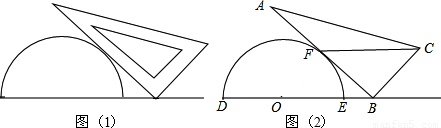
将一个量角器和一个含30度角的直角三角板如图(1)放置,图(2)是由它抽象出的几何图形,其中点B在半圆O的直径DE的延长线上,AB切半圆O于点F,且BC=OD.
(1)求证:DB∥CF;
(2)当OD=2时,若以O、B、F为顶点的三角形与△ABC相似,求OB.
查看答案和解析>>
科目:
来源:第35章《圆(二)》中考题集(13):35.3 探索切线的性质(解析版)
题型:解答题
如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,∠C=20度.求∠CDA的大小.

查看答案和解析>>
科目:
来源:第35章《圆(二)》中考题集(14):35.3 探索切线的性质(解析版)
题型:解答题
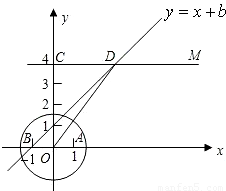
在直角坐标平面内,O为原点,点A的坐标为(1,0),点C的坐标为(0,4),直线CM∥x轴(如图所示).点B与点A关于原点对称,直线y=x+b(b为常数)经过点B,且与直线CM相交于点D,连接OD.
(1)求b的值和点D的坐标;
(2)设点P在x轴的正半轴上,若△POD是等腰三角形,求点P的坐标;
(3)在(2)的条件下,如果以PD为半径的圆P与圆O外切,求圆O的半径.
查看答案和解析>>
科目:
来源:第35章《圆(二)》中考题集(14):35.3 探索切线的性质(解析版)
题型:解答题
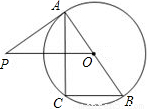
如图,已知AB是⊙O的直径,过点O作弦BC的平行线,交过点A的切线AP于点P,连接AC.
(1)求证:△ABC∽△POA;
(2)若OB=2,OP=

,求BC的长.
查看答案和解析>>
科目:
来源:第35章《圆(二)》中考题集(14):35.3 探索切线的性质(解析版)
题型:解答题
已知,如图,BC是以线段AB为直径的⊙O的切线,AC交⊙O于点D,过点D作弦DE⊥AB,垂足为点F,连接BD、BE.
(1)仔细观察图形并写出四个不同的正确结论:①______,②______,③______,④______(不添加其它字母和辅助线,不必证明);
(2)∠A=30°,CD=
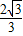
,求⊙O的半径r.

查看答案和解析>>
科目:
来源:第35章《圆(二)》中考题集(14):35.3 探索切线的性质(解析版)
题型:解答题
已知:如图,⊙O的直径AB与弦CD相交于E,
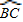
=
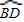
,⊙O的切线BF与弦AD的延长线相交于点F.
(1)求证:CD∥BF.
(2)连接BC,若⊙O的半径为4,cos∠BCD=

,求线段AD、CD的长.

查看答案和解析>>
科目:
来源:第35章《圆(二)》中考题集(14):35.3 探索切线的性质(解析版)
题型:解答题
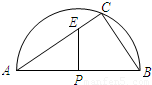
如图,半圆的直径AB=10,点C在半圆上,BC=6.
(1)求弦AC的长;
(2)若P为AB的中点,PE⊥AB交AC于点E,求PE的长.
查看答案和解析>>
科目:
来源:第35章《圆(二)》中考题集(14):35.3 探索切线的性质(解析版)
题型:解答题
如图,矩形ABCD中,AB=5,AD=3.点E是CD上的动点,以AE为直径的⊙O与AB交于点F,过点F作FG⊥BE于点G.
(1)当E是CD的中点时:
①tan∠EAB的值为______;
②证明:FG是⊙O的切线;
(2)试探究:BE能否与⊙O相切?若能,求出此时DE的长;若不能,请说明理由.

查看答案和解析>>
科目:
来源:第35章《圆(二)》中考题集(14):35.3 探索切线的性质(解析版)
题型:解答题
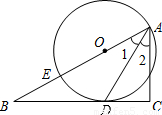
如图,已知点E在△ABC的边AB上,以AE为直径的⊙O与BC相切于点D,且AD平分∠BAC.
求证:AC⊥BC.
查看答案和解析>>





 ,求BC的长.
,求BC的长.
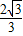 ,求⊙O的半径r.
,求⊙O的半径r.
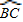 =
=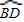 ,⊙O的切线BF与弦AD的延长线相交于点F.
,⊙O的切线BF与弦AD的延长线相交于点F. ,求线段AD、CD的长.
,求线段AD、CD的长.


