相关习题
0 126354 126362 126368 126372 126378 126380 126384 126390 126392 126398 126404 126408 126410 126414 126420 126422 126428 126432 126434 126438 126440 126444 126446 126448 126449 126450 126452 126453 126454 126456 126458 126462 126464 126468 126470 126474 126480 126482 126488 126492 126494 126498 126504 126510 126512 126518 126522 126524 126530 126534 126540 126548 366461
科目:
来源:第35章《圆(二)》中考题集(13):35.3 探索切线的性质(解析版)
题型:解答题
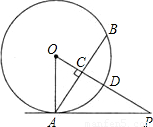
如图,PA与⊙O相切于A点,弦AB⊥OP,垂足为C,OP与⊙O相交于D点,已知OA=2,OP=4.
(1)求∠POA的度数;
(2)计算弦AB的长.
查看答案和解析>>
科目:
来源:第35章《圆(二)》中考题集(13):35.3 探索切线的性质(解析版)
题型:解答题
已知:如图,⊙A与y轴交于C、D两点,圆心A的坐标为(1,0),⊙A的半径为

,过点C作⊙A的切线交x轴于点B(-4,0).
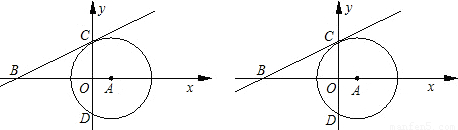
(1)求切线BC的解析式;
(2)若点P是第一象限内⊙A上的一点,过点P作⊙A的切线与直线BC相交于点G,且∠CGP=120°,求点G的坐标;
(3)向左移动⊙A(圆心A始终保持在x轴上),与直线BC交于E、F,在移动过程中是否存在点A,使△AEF是直角三角形?若存在,求出点A的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:
来源:第35章《圆(二)》中考题集(13):35.3 探索切线的性质(解析版)
题型:解答题
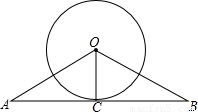
已知:如图,AB与⊙O相切于点C,OA=OB,⊙O的直径为4,AB=8.
(1)求OB的长;
(2)求sinA的值.
查看答案和解析>>
科目:
来源:第35章《圆(二)》中考题集(13):35.3 探索切线的性质(解析版)
题型:解答题
已知:AB是⊙O的弦,D是

的中点,过B作AB的垂线交AD的延长线于C.
(1)求证:AD=DC;
(2)过D作⊙O的切线交BC于E,若DE=EC,求sinC.
查看答案和解析>>
科目:
来源:第35章《圆(二)》中考题集(13):35.3 探索切线的性质(解析版)
题型:解答题
如图,已知AB是⊙O直径,AC是⊙O弦,点D是

的中点,弦DE⊥AB,垂足为F,DE交AC于点G.
(1)若过点E作⊙O的切线ME,交AC的延长线于点M(请补完整图形),试问:ME=MG是否成立?若成立,请证明;若不成立,请说明理由;
(2)在满足第(2)问的条件下,已知AF=3,FB=

,求AG与GM的比.

查看答案和解析>>
科目:
来源:第35章《圆(二)》中考题集(13):35.3 探索切线的性质(解析版)
题型:解答题
如图1,已知O是锐角∠XAY的边AX上的动点,以点O为圆心、R为半径的圆与射线AY切于点B,交射线OX于点C,连接BC,作CD⊥BC,交AY于点D.
(1)求证:△ABC∽△ACD;
(2)若P是AY上一点,AP=4,且sinA=

,
①如图2,当点D与点P重合时,求R的值;
②当点D与点P不重合时,试求PD的长(用R表示).
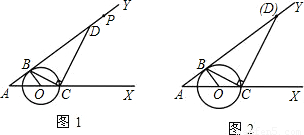
查看答案和解析>>
科目:
来源:第35章《圆(二)》中考题集(13):35.3 探索切线的性质(解析版)
题型:解答题
如图,⊙O的直径AB=2,AM和BN是它的两条切线,DE切⊙O于E,交AM于D,交BN于C.设AD=x,BC=y.
(1)求证:AM∥BN;
(2)求y关于x的关系式;
(3)求四边形ABCD的面积S,并证明:S≥2.

查看答案和解析>>
科目:
来源:第35章《圆(二)》中考题集(13):35.3 探索切线的性质(解析版)
题型:解答题
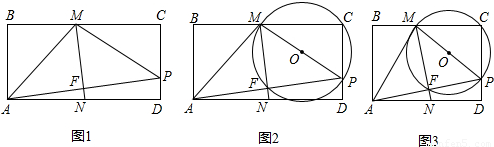
已知:如图1,把矩形纸片ABCD折叠,使得顶点A与边DC上的动点P重合(P不与点D,C重合),MN为折痕,点M,N分别在边BC,AD上,连接AP,MP,AM,AP与MN相交于点F.⊙O过点M,C,P.
(1)请你在图1中作出⊙O(不写作法,保留作图痕迹);
(2)
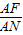
与
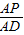
是否相等?请你说明理由;
(3)随着点P的运动,若⊙O与AM相切于点M时,⊙O又与AD相切于点H.设AB为4,请你通过计算,画出这时的图形.(图2,3供参考)
查看答案和解析>>
科目:
来源:第35章《圆(二)》中考题集(13):35.3 探索切线的性质(解析版)
题型:解答题
如图,AB,BC分别是⊙O的直径和弦,点D为

上一点,弦DE交⊙O于点E,交AB于点F,交BC于点G,过点C的切线交ED的延长线于H,且HC=HG,连接BH,交⊙O于点M,连接MD,ME.
求证:
(1)DE⊥AB;
(2)∠HMD=∠MHE+∠MEH.
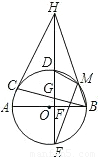
查看答案和解析>>
科目:
来源:第35章《圆(二)》中考题集(13):35.3 探索切线的性质(解析版)
题型:解答题
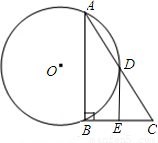
如图,在Rt△ABC中,斜边BC=12,∠C=30°,D为BC的中点,△ABD的外接圆⊙O与AC交于F点,过A作⊙O的切线AE交DF的延长线于E点.
(1)求证:AE⊥DE;
(2)计算:AC•AF的值.
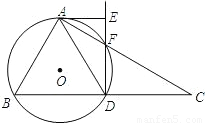
查看答案和解析>>


 ,过点C作⊙A的切线交x轴于点B(-4,0).
,过点C作⊙A的切线交x轴于点B(-4,0).

 的中点,过B作AB的垂线交AD的延长线于C.
的中点,过B作AB的垂线交AD的延长线于C.
 的中点,弦DE⊥AB,垂足为F,DE交AC于点G.
的中点,弦DE⊥AB,垂足为F,DE交AC于点G. ,求AG与GM的比.
,求AG与GM的比.
 ,
,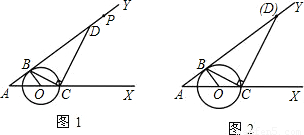

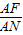 与
与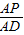 是否相等?请你说明理由;
是否相等?请你说明理由;
 上一点,弦DE交⊙O于点E,交AB于点F,交BC于点G,过点C的切线交ED的延长线于H,且HC=HG,连接BH,交⊙O于点M,连接MD,ME.
上一点,弦DE交⊙O于点E,交AB于点F,交BC于点G,过点C的切线交ED的延长线于H,且HC=HG,连接BH,交⊙O于点M,连接MD,ME.
