相关习题
0 126355 126363 126369 126373 126379 126381 126385 126391 126393 126399 126405 126409 126411 126415 126421 126423 126429 126433 126435 126439 126441 126445 126447 126449 126450 126451 126453 126454 126455 126457 126459 126463 126465 126469 126471 126475 126481 126483 126489 126493 126495 126499 126505 126511 126513 126519 126523 126525 126531 126535 126541 126549 366461
科目:
来源:第35章《圆(二)》中考题集(13):35.3 探索切线的性质(解析版)
题型:解答题
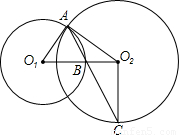
如图,已知⊙O
1与⊙O
2都过点A,AO
1是⊙O
2的切线,⊙O
1交O
1O
2于点B,连接AB并延长交⊙O
2于点C,连接O
2C.
(1)求证:O
2C⊥O
1O
2;
(2)证明:AB•BC=2O
2B•BO
1;
(3)如果AB•BC=12,O
2C=4,求AO
1的长.
查看答案和解析>>
科目:
来源:第35章《圆(二)》中考题集(13):35.3 探索切线的性质(解析版)
题型:解答题
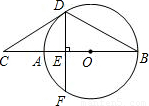
如图,AB是⊙O的直径,点C在BA的延长线上,直线CD与⊙O相切于点D,弦DF⊥AB于点E,线段CD=10,连接BD.
(1)求证:∠CDE=2∠B;
(2)若BD:AB=
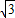
:2,求⊙O的半径及DF的长.
查看答案和解析>>
科目:
来源:第35章《圆(二)》中考题集(13):35.3 探索切线的性质(解析版)
题型:解答题
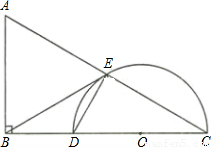
如图,在Rt△ABC中∠ABC=90°,斜边AC的垂直平分线交BC与D点,交AC于E点,连接BE.
(1)若BE是△DEC的外接圆⊙O的切线,求∠C的大小;
(2)当AB=1,BC=2时,求△DEC外接圆的半径.
查看答案和解析>>
科目:
来源:第35章《圆(二)》中考题集(13):35.3 探索切线的性质(解析版)
题型:解答题
如图,BD是⊙O的弦.过点D作⊙O的切线交BO延长线于点A.AC⊥AD交BD延长线于点C.
(1)求证:AB=AC;
(2)若AB=5,∠B=25°.求AD的长.(精确到0.1)

查看答案和解析>>
科目:
来源:第35章《圆(二)》中考题集(13):35.3 探索切线的性质(解析版)
题型:解答题
如图,AB为⊙O的直径,弦CD⊥AB,垂足为点M,AE切⊙O于点A,交BC的延长线于点E,连接AC.
(1)若∠B=30°,AB=2,求CD的长;
(2)求证:AE
2=EB•EC.

查看答案和解析>>
科目:
来源:第35章《圆(二)》中考题集(13):35.3 探索切线的性质(解析版)
题型:解答题
如图所示,已知AB是⊙O的直径,直线L与⊙O相切于点C,
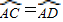
,CD交AB于E,BF⊥直线L,垂足为F,BF交⊙O于C.
(1)图中哪条线段与AE相等?试证明你的结论;
(2)若

,AE=4,求AB的值.
查看答案和解析>>
科目:
来源:第35章《圆(二)》中考题集(13):35.3 探索切线的性质(解析版)
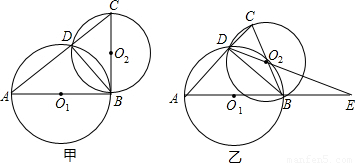
题型:解答题
在△ABC中,分别以AB、BC为直径的⊙O
1、⊙O
2,交于另一点D.
(1)证明:交点D必在AC上;
(2)如图甲,当⊙O
1与⊙O
2半径之比为4:3,且DO
2与⊙O
1相切时,判断△ABC的形状,并求tan∠O
2DB的值;
(3)如图乙,当⊙O
1经过点O
2,AB、DO
2的延长线交于E,且BE=BD时,求∠A的度数.
查看答案和解析>>
科目:
来源:第35章《圆(二)》中考题集(13):35.3 探索切线的性质(解析版)
题型:解答题
如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,过点D的切线交BC于E.
(1)求证:DE=

BC;
(2)若tanC=
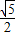
,DE=2,求AD的长.

查看答案和解析>>
科目:
来源:第35章《圆(二)》中考题集(13):35.3 探索切线的性质(解析版)
题型:解答题
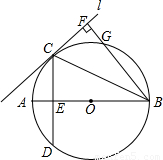
(1)如图1,PA,PB分别与圆O相切于点A,B.求证:PA=PB;
(2)如图2,过圆O外一点P的两条直线分别与圆O相交于点A、B和C、D.则当______时,PB=PD.(不添加字母符号和辅助线,不需证明,只需填上符合题意的一个条件)
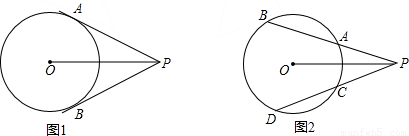
查看答案和解析>>
科目:
来源:第35章《圆(二)》中考题集(13):35.3 探索切线的性质(解析版)
题型:解答题
如图,⊙O是△ABC的外接圆,FH是⊙O的切线,切点为F,FH∥BC,连接AF交BC于E,∠ABC的平分线BD交AF于D,连接BF.
(1)证明:AF平分∠BAC;
(2)证明:BF=FD;
(3)若EF=4,DE=3,求AD的长.
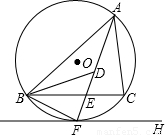
查看答案和解析>>


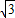 :2,求⊙O的半径及DF的长.
:2,求⊙O的半径及DF的长.



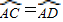 ,CD交AB于E,BF⊥直线L,垂足为F,BF交⊙O于C.
,CD交AB于E,BF⊥直线L,垂足为F,BF交⊙O于C. ,AE=4,求AB的值.
,AE=4,求AB的值.

 BC;
BC;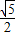 ,DE=2,求AD的长.
,DE=2,求AD的长.

