
科目: 来源:第34章《二次函数》常考题集(15):34.4 二次函数的应用(解析版) 题型:选择题
 x2+
x2+ x+
x+ ,绳子甩到最高处时刚好通过站在x=2点处跳绳的学生小明的头顶,则小明的身高为( )
,绳子甩到最高处时刚好通过站在x=2点处跳绳的学生小明的头顶,则小明的身高为( )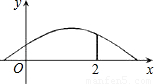
查看答案和解析>>
科目: 来源:第34章《二次函数》常考题集(15):34.4 二次函数的应用(解析版) 题型:选择题
 x2+2的图象在x轴上方的一部分,对于这段图象与x轴所围成的阴影部分的面积,你认为可能的值是( )
x2+2的图象在x轴上方的一部分,对于这段图象与x轴所围成的阴影部分的面积,你认为可能的值是( )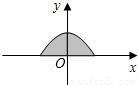
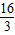
查看答案和解析>>
科目: 来源:第34章《二次函数》常考题集(15):34.4 二次函数的应用(解析版) 题型:选择题
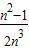 ,S2=
,S2=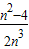 ,…;记W=S1+S2+…+Sn-1,当n越来越大时,你猜想W最接近的常数是( )
,…;记W=S1+S2+…+Sn-1,当n越来越大时,你猜想W最接近的常数是( )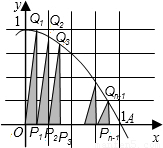




查看答案和解析>>
科目: 来源:第34章《二次函数》常考题集(15):34.4 二次函数的应用(解析版) 题型:选择题
 ≤a≤1
≤a≤1 ≤a≤2
≤a≤2 ≤a≤1
≤a≤1 ≤a≤2
≤a≤2查看答案和解析>>
科目: 来源:第34章《二次函数》常考题集(15):34.4 二次函数的应用(解析版) 题型:选择题
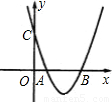
查看答案和解析>>
科目: 来源:第34章《二次函数》常考题集(15):34.4 二次函数的应用(解析版) 题型:选择题
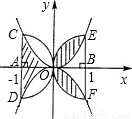
 π
π π
π查看答案和解析>>
科目: 来源:第34章《二次函数》常考题集(15):34.4 二次函数的应用(解析版) 题型:选择题
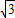 的斜坡笔直滑下,滑下的距离s(米)与时间t(秒)间的关系为s=10t+2t2,若滑到坡底的时间为4秒,则此人下降的高度为( )
的斜坡笔直滑下,滑下的距离s(米)与时间t(秒)间的关系为s=10t+2t2,若滑到坡底的时间为4秒,则此人下降的高度为( )
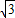 m
m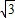 m
m查看答案和解析>>
科目: 来源:第34章《二次函数》常考题集(15):34.4 二次函数的应用(解析版) 题型:选择题
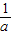 <
<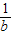 ;③对角线相等且互相垂直的四边形是正方形;④抛物线y=x2-2x与坐标轴有3个不同交点;⑤已知一圆锥的高为4,母线长为5,则该圆锥的侧面积为15π.从中任选一个命题是真命题的概率为( )
;③对角线相等且互相垂直的四边形是正方形;④抛物线y=x2-2x与坐标轴有3个不同交点;⑤已知一圆锥的高为4,母线长为5,则该圆锥的侧面积为15π.从中任选一个命题是真命题的概率为( )



查看答案和解析>>
科目: 来源:第34章《二次函数》常考题集(15):34.4 二次函数的应用(解析版) 题型:填空题
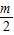 与x轴的一个交点的坐标为(1,0),则此抛物线与x轴的另一个交点的坐标是 .
与x轴的一个交点的坐标为(1,0),则此抛物线与x轴的另一个交点的坐标是 .查看答案和解析>>
科目: 来源:第34章《二次函数》常考题集(15):34.4 二次函数的应用(解析版) 题型:填空题
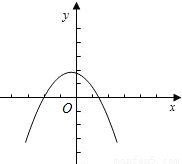
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com