相关习题
0 126453 126461 126467 126471 126477 126479 126483 126489 126491 126497 126503 126507 126509 126513 126519 126521 126527 126531 126533 126537 126539 126543 126545 126547 126548 126549 126551 126552 126553 126555 126557 126561 126563 126567 126569 126573 126579 126581 126587 126591 126593 126597 126603 126609 126611 126617 126621 126623 126629 126633 126639 126647 366461
科目:
来源:第34章《二次函数》中考题集(50):34.4 二次函数的应用(解析版)
题型:解答题
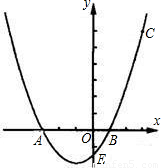
如图,抛物线y=ax
2+bx+c经过A(-3,0),B(1,0),C(3,6)三点,且与y轴交于点E.(1)求抛物线的解析式;
(2)若点F的坐标为(0,-

),直线BF交抛物线于另一点P,试比较△AFO与△PEF的周长的大小,并说明理由.
查看答案和解析>>
科目:
来源:第34章《二次函数》中考题集(50):34.4 二次函数的应用(解析版)
题型:解答题
已知二次函数y=ax2-4a图象的顶点坐标为(0,4)矩形ABCD在抛物线与x轴围成的图形内,顶点B、C在x轴上,顶点A、D在抛物线上,且A在D点的右侧,
(1)求二次函数的解析式______;
(2)设点A的坐标为(x,y),试求矩形ABCD的周长L与自变量x的函数关系;
(3)周长为10的矩形ABCD是否存在?若存在,请求出顶点A的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:
来源:第34章《二次函数》中考题集(50):34.4 二次函数的应用(解析版)
题型:解答题
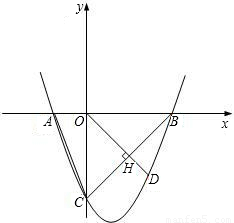
已知二次函数y=x
2-kx+k-5.
(1)求证:无论k取何实数,此二次函数的图象与x轴都有两个交点;
(2)若此二次函数图象的对称轴为x=1,求它的解析式;
(3)若(2)中的二次函数的图象与x轴交于A、B,与y轴交于点C;D是第四象限函数图象上的点,且OD⊥BC于H,求点D的坐标.
查看答案和解析>>
科目:
来源:第34章《二次函数》中考题集(50):34.4 二次函数的应用(解析版)
题型:解答题
已知:如图,抛物线y=

x
2-
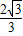
x+m与x轴交于A、B两点,与y轴交于C点,∠ACB=90°,
(1)求m的值及抛物线顶点坐标;
(2)过A、B、C的三点的⊙M交y轴于另一点D,连接DM并延长交⊙M于点E,过E点的⊙M的切线分别交x轴、y轴于点F、G,求直线FG的解析式;
(3)在条件(2)下,设P为

上的动点(P不与C、D重合),连接PA交y轴于点H,问是否存在一个常数k,始终满足AH•AP=k?如果存在,请写出求解过程;如果不存在,请说明理由.

查看答案和解析>>
科目:
来源:第34章《二次函数》中考题集(50):34.4 二次函数的应用(解析版)
题型:解答题
如图,在平面直角坐标系中有一直角梯形OABC,∠AOC=90°,AB∥OC,OC在x轴上,过A、B、C三点的抛物线表达式为

.
(1)求A、B、C三点的坐标;
(2)如果在梯形OABC内有一矩形MNPO,使M在y轴上,N在BC边上,P在OC边上,当MN为多少时,矩形MNPO的面积最大?最大面积是多少?
(3)若用一条直线将梯形OABC分为面积相等的两部分,试说明你的分法.

查看答案和解析>>
科目:
来源:第34章《二次函数》中考题集(50):34.4 二次函数的应用(解析版)
题型:解答题
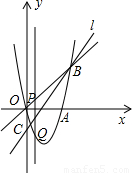
如图,抛物线y=ax
2+bx+c经过点O(0,0),A(4,0),B(5,5).点C是y轴负半轴上一点,直线l经过B,C两点,且tan∠OCB=

.
(1)求抛物线的解析式;
(2)求直线l的解析式;
(3)过O,B两点作直线,如果P是直线OB上的一个动点,过点P作直线PQ平行于y轴,交抛物线于点Q.问:是否存在点P,使得以P,Q,B为顶点的三角形与△OBC相似?如果存在,请求出点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:
来源:第34章《二次函数》中考题集(50):34.4 二次函数的应用(解析版)
题型:解答题
已知抛物线y=-(x-m)
2+1与x轴的交点为A、B(B在A的右边),与y轴的交点为C.
(1)写出m=1时与抛物线有关的三个正确结论;
(2)当点B在原点的右边,点C在原点的下方时,是否存在△BOC为等腰三角形的情形?若存在,求出m的值;若不存在,请说明理由;
(3)请你提出一个对任意的m值都能成立的正确命题(说明:根据提出问题的水平层次,得分略有差异).
查看答案和解析>>
科目:
来源:第34章《二次函数》中考题集(50):34.4 二次函数的应用(解析版)
题型:解答题
在以O为原点的平面直角坐标系中,抛物线y=ax
2+bx+c(a≠0)与y轴交于点C(0,3),与x轴正半轴交于A、B两点(B在A点的右侧),抛物线的对称轴是x=2,且S
△AOC=

.
(1)求此抛物线的解析式;
(2)设此抛物线的顶点为D,求四边形ADBC的面积.
查看答案和解析>>
科目:
来源:第34章《二次函数》中考题集(51):34.4 二次函数的应用(解析版)
题型:解答题
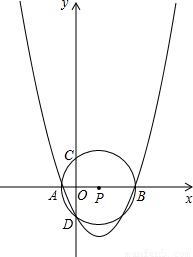
已知⊙P的圆心坐标为(1.5,0),半径为2.5,⊙P与x轴交于A、B两点(点A在点B的左侧),与y轴的负半轴交于点D.
(1)求D点的坐标;
(2)求过A、B、D三点的抛物线的解析式;
(3)设平行于x轴的直线交此抛物线于E、F两点,问:是否存在以线段EF为直径的圆O'恰好与⊙P相外切?若存在,求出其半径r及圆心O'的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:
来源:第34章《二次函数》中考题集(51):34.4 二次函数的应用(解析版)
题型:解答题
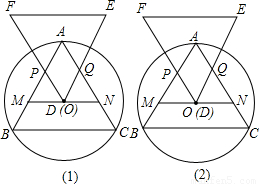
如图(1),已知圆O是等边△ABC的外接圆,过O点作MN∥BC分别交AB、AC于M、N,且MN=a.另一个与△ABC全等的等边△DEF的顶点D在MN上移动(不与点M、N重合),并始终保持EF∥BC,DF交AB于点P,DE交AC于点Q.
(1)试判断四边形APDQ的形状,并进行证明;
(2)设DM为x,四边形APDQ的面积为y,试探究y与x的函数关系式;四边形APDQ的面积能取到最大值吗?如果能,请求出它的最大值,并确定此时D点的位置.
(3)如图(2),当D点和圆心O重合时,请判断四边形APDQ的形状,并说明理由;你能发现四边形APDQ的面积与△ABC的面积有何关系吗?为什么?
查看答案和解析>>

 ),直线BF交抛物线于另一点P,试比较△AFO与△PEF的周长的大小,并说明理由.
),直线BF交抛物线于另一点P,试比较△AFO与△PEF的周长的大小,并说明理由.
 已知二次函数y=x2-kx+k-5.
已知二次函数y=x2-kx+k-5. x2-
x2-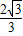 x+m与x轴交于A、B两点,与y轴交于C点,∠ACB=90°,
x+m与x轴交于A、B两点,与y轴交于C点,∠ACB=90°, 上的动点(P不与C、D重合),连接PA交y轴于点H,问是否存在一个常数k,始终满足AH•AP=k?如果存在,请写出求解过程;如果不存在,请说明理由.
上的动点(P不与C、D重合),连接PA交y轴于点H,问是否存在一个常数k,始终满足AH•AP=k?如果存在,请写出求解过程;如果不存在,请说明理由.
 .
.
 .
.

 .
.
