相关习题
0 126458 126466 126472 126476 126482 126484 126488 126494 126496 126502 126508 126512 126514 126518 126524 126526 126532 126536 126538 126542 126544 126548 126550 126552 126553 126554 126556 126557 126558 126560 126562 126566 126568 126572 126574 126578 126584 126586 126592 126596 126598 126602 126608 126614 126616 126622 126626 126628 126634 126638 126644 126652 366461
科目：
来源：第34章《二次函数》中考题集（49）：34.4 二次函数的应用（解析版）
题型：解答题
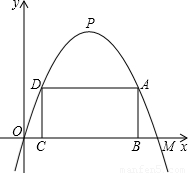
如图所示，在平面直角坐标中，抛物线的顶点P到x轴的距离是4，抛物线与x轴相交于O、M两点，OM=4；矩形ABCD的边BC在线段的OM上，点A、D在抛物线上．
（1）请写出P、M两点坐标，并求出这条抛物线的解析式；
（2）设矩形ABCD的周长为l，求l的最大值；
（3）连接OP、PM，则△PMO为等腰三角形，请判断在抛物线上是否存在点Q（除点M外），使得△OPQ也是等腰三角形，简要说明你的理由．
查看答案和解析>>
科目：
来源：第34章《二次函数》中考题集（49）：34.4 二次函数的应用（解析版）
题型：解答题
已知二次函数的图象经过（0，0），（1，-1），（-2，14）三点．
（1）求这个二次函数的解析式；
（2）设这个二次函数的图象与直线y=x+t（t≤1）相交于（x1，y1），（x2，y2）两点（x1≠x2）．
①求t的取值范围；
②设m=y12+y22，求m与t之间的函数关系式及m的取值范围．
查看答案和解析>>
科目：
来源：第34章《二次函数》中考题集（49）：34.4 二次函数的应用（解析版）
题型：解答题
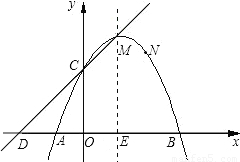
如图，已知抛物线的顶点坐标为M（1，4），且经过点N（2，3），与x轴交于A、B两点（点A在点B左侧），与y轴交于点C．
（1）求抛物线的解析式及点A、B、C的坐标；
（2）若直线y=kx+t经过C、M两点，且与x轴交于点D，试证明四边形CDAN是平行四边形；
（3）点P在抛物线的对称轴x=1上运动，请探索：在x轴上方是否存在这样的P点，使以P为圆心的圆经过A、B两点，并且与直线CD相切？若存在，请求出点P的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：
来源：第34章《二次函数》中考题集（49）：34.4 二次函数的应用（解析版）
题型：解答题
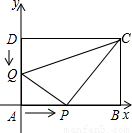
已知：如图，在坐标平面内，A（0，0），B（12，0），C（12，6），D（0，6），点Q沿DA边从点D开始向点A以1单位/秒的速度移动．点P沿AB边从点A开始向B以2单位/秒的速度移动，假设P、Q同时出发，t表示移动的时间（0≤t≤6）．
（1）写出△PQA的面积S与t的函数关系式；
（2）四边形APCQ的面积与t有关吗？请说明理由；（3）当t为何值时，△PQC面积最小，并求此时△PQC的面积；
（4）△APQ能否成轴对称图形？若能，请求出相应的t值，并写出其对称轴的函数关系式；若不能，请说明理由．
查看答案和解析>>
科目：
来源：第34章《二次函数》中考题集（49）：34.4 二次函数的应用（解析版）
题型：解答题
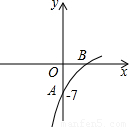
已知抛物线y=（1-a）x
2+8x+b的图象的一部分如图所示，抛物的顶点在第一象限，且经过点A（0，-7）和点B．
（1）求a的取值范围；
（2）若OA=2OB，求抛物线的解析式．
查看答案和解析>>
科目：
来源：第34章《二次函数》中考题集（49）：34.4 二次函数的应用（解析版）
题型：解答题
已知，如图，在直角坐标系中O是坐标原点，四边形AOCB是矩形，0C=6，OA=2，P是边AB上的任意一点．当点P在边AB上移动时，是否存在这样的点P使得OP⊥PC成立？若存在，请求出点P的坐标，画出满足条件的P点，并求出经过D、P、C三点的抛物线的对称轴；若不存在这样的P点，请说明理由．
查看答案和解析>>
科目：
来源：第34章《二次函数》中考题集（49）：34.4 二次函数的应用（解析版）
题型：解答题
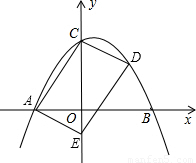
如图，抛物线y=-
x
2+
x+6，与x轴交于A、B两点，与y轴相交于C点．
（1）求△ABC的面积；
（2）已知E点（0，-3），在第一象限的抛物线上取点D，连接DE，使DE被x轴平分，试判定四边形ACDE的形状，并证明你的结论．
查看答案和解析>>
科目：
来源：第34章《二次函数》中考题集（49）：34.4 二次函数的应用（解析版）
题型：解答题
已知抛物线y=x2+bx-a2．
（1）请你选定a、b适当的值，然后写出这条抛物线与坐标轴的三个交点，并画出过三个交点的圆；
（2）试讨论此抛物线与坐标轴交点分别是1个，2个，3个时，a、b的取值范围，并且求出交点坐标．
查看答案和解析>>
科目：
来源：第34章《二次函数》中考题集（49）：34.4 二次函数的应用（解析版）
题型：解答题
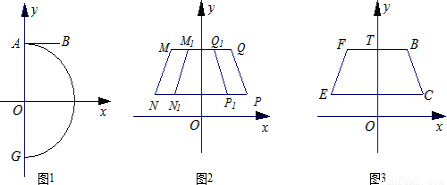
已知：以原点O为圆心、5为半径的半圆与y轴交于A、G两点，AB与半圆相切于点A，点B的坐标为（3，y
B）（如图1）；过半圆上的点C（x
C，y
C）作y轴的垂线，垂足为D；Rt△DOC的面积等于
x
C2．
（1）求点C的坐标；
（2）①命题“如图2，以y轴为对称轴的等腰梯形MNPQ与M
1N
1P
1Q
1的上底和下底都分别在同一条直线上，NP∥MQ，PQ∥P
1Q
1，且NP＞MQ．设抛物线y=a
x
2+h
过点P、Q，抛物线y=a
1x
2+h
1过点P
1、Q
1，则h
＞h
1”是真命题．请你以Q（3，5）、P（4，3）和Q
1（p，5）、P
1（p+1，3）为例进行验证；
②当图1中的线段BC在第一象限时，作线段BC关于y轴对称的线段FE，连接BF、CE，点T是线段BF上的动点（如图3）；设K是过T、B、C三点的抛物线y=ax
2+bx+c的顶点，求K的纵坐标y
K的取值范围．
查看答案和解析>>
科目：
来源：第34章《二次函数》中考题集（49）：34.4 二次函数的应用（解析版）
题型：解答题
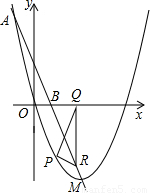
如图，已知抛物线的顶点为M（2，-4），且过点A（-1，5），连接AM交x轴于点B．
（1）求这条抛物线的解析式；
（2）求点B的坐标；
（3）设点P（x，y）是抛物线在x轴下方、顶点左方一段上的动点，连接PO，以P为顶点、PO为腰的等腰三角形的另一顶点Q在x轴的垂线交直线AM于点R，连接PR，设△PQR的面积为S，求S与x之间的函数关系式；
（4）在上述动点P（x，y）中，是否存在使S
△PQR=2的点？若存在，求点P的坐标；若不存在，说明理由．
查看答案和解析>>
