相关习题
0 126462 126470 126476 126480 126486 126488 126492 126498 126500 126506 126512 126516 126518 126522 126528 126530 126536 126540 126542 126546 126548 126552 126554 126556 126557 126558 126560 126561 126562 126564 126566 126570 126572 126576 126578 126582 126588 126590 126596 126600 126602 126606 126612 126618 126620 126626 126630 126632 126638 126642 126648 126656 366461
科目:
来源:第34章《二次函数》中考题集(44):34.4 二次函数的应用(解析版)
题型:解答题
已知抛物线y=ax
2+bx+2与x轴相交于点A(x
1,0),B(x
2,0)(x
1<x
2),且x
1,x
2是方程x
2-2x-3=0的两个实数根,点C为抛物线与y轴的交点.
(1)求a,b的值;
(2)分别求出直线AC和BC的解析式;
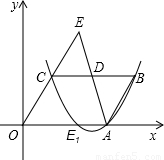
(3)若动直线y=m(0<m<2)与线段AC,BC分别相交于D,E两点,则在x轴上是否存在点P,使得△DEP为等腰直角三角形?若存在,求出点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:
来源:第34章《二次函数》中考题集(44):34.4 二次函数的应用(解析版)
题型:解答题
如图,在直角坐标系中,O为坐标原点,平行四边形OABC的边OA在x轴上,∠B=60°,OA=6,OC=4,D是BC的中点,延长AD交OC的延长线于点E.
(1)画出△ECD关于边CD所在直线为对称轴的对称图形△E
1CD,并求出点E
1的坐标;
(2)求经过C、E
1、B三点的抛物线的函数表达式;
(3)请探求经过C、E
1、B三点的抛物线上是否存在点P,使以点P、B、C为顶点的三角形与△ECD相似?若存在这样的点P,请求出点P的坐标;若不存在这样的点P,请说明理由.
查看答案和解析>>
科目:
来源:第34章《二次函数》中考题集(44):34.4 二次函数的应用(解析版)
题型:解答题
如图,边长为4的正方形OABC的顶点O为坐标原点,点A在x轴的正半轴上,点C在y轴的正半轴上.动点D在线段BC上移动(不与B,C重合),连接OD,过点D作DE⊥OD,交边AB于点E,连接OE.
(1)当CD=1时,求点E的坐标;
(2)如果设CD=t,梯形COEB的面积为S,那么是否存在S的最大值?若存在,请求出这个最大值及此时t的值;若不存在,请说明理由.

查看答案和解析>>
科目:
来源:第34章《二次函数》中考题集(44):34.4 二次函数的应用(解析版)
题型:解答题
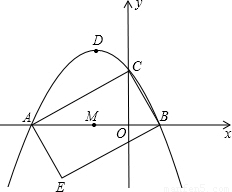
如图抛物线y=
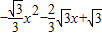
,x轴于A、B两点,交y轴于点C,顶点为D.
(1)求A、B、C的坐标;
(2)把△ABC绕AB的中点M旋转180°,得到四边形AEBC:
①求E点坐标;
②试判断四边形AEBC的形状,并说明理由;
(3)试探索:在直线BC上是否存在一点P,使得△PAD的周长最小?若存在,请求出P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:
来源:第34章《二次函数》中考题集(44):34.4 二次函数的应用(解析版)
题型:解答题
如图,直线y=-

x+2与x轴交于点C,与y轴交于点B,点A为y轴正半轴上的一点,⊙A经过点B,O,直线BC交⊙A于点D.
(1)求点D的坐标.
(2)以OC为直径作⊙O',连接AD,直线AD与⊙O'相切吗?为什么?
(3)过O,C,D三点作抛物线,在抛物线的对称轴上是否存在一点P,使线段PO与PD之差的值最大?若存在,请求出这个最大值和点P的坐标,若不存在,请说明理由.

查看答案和解析>>
科目:
来源:第34章《二次函数》中考题集(44):34.4 二次函数的应用(解析版)
题型:解答题
(附加题)已知抛物线y=x
2+kx+b经过点P(2,-3),Q(-1,0).
(1)求抛物线的解析式;
(2)设抛物线顶点为N,与y轴交点为A.求sin∠AON的值;
(3)设抛物线与x轴的另一个交点为M,求四边形OANM的面积.

查看答案和解析>>
科目:
来源:第34章《二次函数》中考题集(44):34.4 二次函数的应用(解析版)
题型:解答题
如图,已知抛物线y=-x
2+mx+3与x轴的一个交点A(3,0).
(1)你一定能分别求出这条抛物线与x轴的另一个交点B及与y轴的交点C的坐标,试试看;
(2)设抛物线的顶点为D,请在图中画出抛物线的草图.若点E(-2,n)在直线BC上,试判断E点是否在经过D点的反比例函数的图象上,把你的判断过程写出来;
(3)请设法求出tan∠DAC的值.
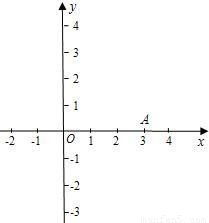
查看答案和解析>>
科目:
来源:第34章《二次函数》中考题集(44):34.4 二次函数的应用(解析版)
题型:解答题
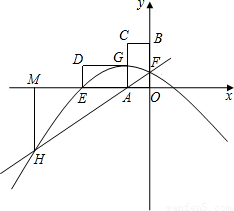
如图,点O是坐标原点,点A(n,0)是x轴上一动点(n<0).以AO为一边作矩形AOBC,点C在第二象限,且OB=2OA.矩形AOBC绕点A逆时针旋转90°得矩形AGDE.过点A的直线y=kx+m交y轴于点F,FB=FA.抛物线y=ax
2+bx+c过点E、F、G且和直线AF交于点H,过点H作HM⊥x轴,垂足为点M.
(1)求k的值;
(2)点A位置改变时,△AMH的面积和矩形AOBC的面积的比值是否改变?说明你的理由.
查看答案和解析>>
科目:
来源:第34章《二次函数》中考题集(47):34.4 二次函数的应用(解析版)
题型:解答题
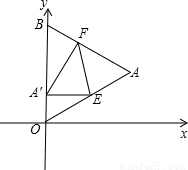
如图,△OAB是边长为2+

的等边三角形,其中O是坐标原点,顶点B在y轴正方向上,将△OAB折叠,使点A落在边OB上,记为A′,折痕为EF.
(1)当A′E∥x轴时,求点A′和E的坐标;
(2)当A′E∥x轴,且抛物线y=-

x
2+bx+c经过点A′和E时,求抛物线与x轴的交点的坐标;
(3)当点A′在OB上运动,但不与点O、B重合时,能否使△A′EF成为直角三角形?若能,请求出此时点A′的坐标;若不能,请你说明理由.
查看答案和解析>>
科目:
来源:第34章《二次函数》中考题集(47):34.4 二次函数的应用(解析版)
题型:解答题
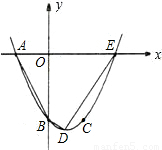
如图,已知抛物线y=ax
2+bx+c(a≠0)经过A(-2,0),B(0,-4),C(2,-4)三点,且与x轴的另一个交点为E.
(1)求抛物线的解析式;
(2)用配方法求抛物线的顶点D的坐标和对称轴;
(3)求四边形ABDE的面积.
查看答案和解析>>




 如图抛物线y=
如图抛物线y=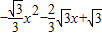 ,x轴于A、B两点,交y轴于点C,顶点为D.
,x轴于A、B两点,交y轴于点C,顶点为D. x+2与x轴交于点C,与y轴交于点B,点A为y轴正半轴上的一点,⊙A经过点B,O,直线BC交⊙A于点D.
x+2与x轴交于点C,与y轴交于点B,点A为y轴正半轴上的一点,⊙A经过点B,O,直线BC交⊙A于点D.

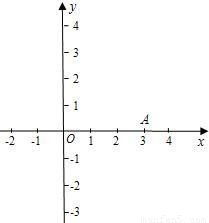

 的等边三角形,其中O是坐标原点,顶点B在y轴正方向上,将△OAB折叠,使点A落在边OB上,记为A′,折痕为EF.
的等边三角形,其中O是坐标原点,顶点B在y轴正方向上,将△OAB折叠,使点A落在边OB上,记为A′,折痕为EF. x2+bx+c经过点A′和E时,求抛物线与x轴的交点的坐标;
x2+bx+c经过点A′和E时,求抛物线与x轴的交点的坐标;
