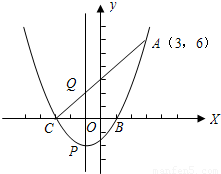相关习题
0 126465 126473 126479 126483 126489 126491 126495 126501 126503 126509 126515 126519 126521 126525 126531 126533 126539 126543 126545 126549 126551 126555 126557 126559 126560 126561 126563 126564 126565 126567 126569 126573 126575 126579 126581 126585 126591 126593 126599 126603 126605 126609 126615 126621 126623 126629 126633 126635 126641 126645 126651 126659 366461
科目:
来源:第34章《二次函数》中考题集(43):34.4 二次函数的应用(解析版)
题型:解答题
如图,已知抛物线y=-x
2+2x+3交轴于A,B两点(点A在点B的左侧),与y轴交于点C
(1)求点A、B、C的坐标;
(2)若点M为抛物线的顶点,连接BC、CM、BM,求△BCM的面积;
(3)连接AC,在轴上是否存在点P,使△ACP为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:
来源:第34章《二次函数》中考题集(43):34.4 二次函数的应用(解析版)
题型:解答题
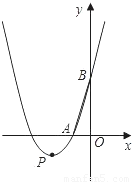
如图,在直角坐标系中,O为原点,抛物线y=x
2+bx+3与x轴的负半轴交于点A,与y轴的正半轴交于点B,tan∠ABO=

,顶点为P.
(1)求抛物线的解析式;
(2)若抛物线向上或向下平移|k|个单位长度后经过点C(-5,6),试求k的值及平移后抛物线的最小值;
(3)设平移后的抛物线与y轴相交于D,顶点为Q,点M是平移的抛物线上的一个动点.请探究:当点M在何位置时,△MBD的面积是△MPQ面积的2倍求出此时点M的坐标.友情提示:抛物线y=ax
2+bx+c(a≠0)的对称轴是
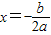
,顶点坐标是
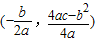
.
查看答案和解析>>
科目:
来源:第34章《二次函数》中考题集(43):34.4 二次函数的应用(解析版)
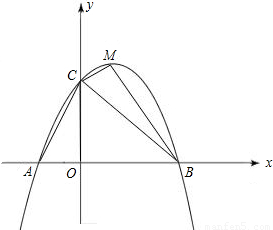
题型:解答题
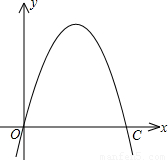
如图,抛物线y=-x
2+2nx+n
2-9(n为常数)经过坐标原点和x轴上另一点C,顶点在第一象限.
(1)确定抛物线所对应的函数关系式,并写出顶点坐标;
(2)在四边形OABC内有一矩形MNPQ,点M,N分别在OA,BC上,A点坐标为(2,8)B点坐标为(4,8),点Q,P在x轴上.当MN为多少时,矩形MNPQ的面积最大,最大面积是多少?
查看答案和解析>>
科目:
来源:第34章《二次函数》中考题集(43):34.4 二次函数的应用(解析版)
题型:解答题
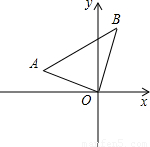
在平面直角坐标系中,△AOB的位置如图所示,已知∠AOB=90°,AO=BO,点A的坐标为(-3,1).
(1)求点B的坐标;
(2)求过A,O,B三点的抛物线的解析式;
(3)设点B关于抛物线的对称轴l的对称点为B
1,求△AB
1B的面积.
查看答案和解析>>
科目:
来源:第34章《二次函数》中考题集(43):34.4 二次函数的应用(解析版)
题型:解答题
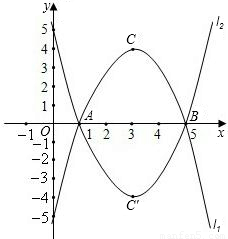
如图,已知与x轴交于点A(1,0)和B(5,0)的抛物线的顶点为C(3,4),抛物线l
2与l
1关于x轴对称,顶点为C′.
(1)求抛物线l
2的函数关系式;
(2)已知原点O,定点D(0,4),l
2上的点P与l
1上的点P′始终关于x轴对称,则当点P运动到何处时,以点D,O,P,P′为顶点的四边形是平行四边形;
(3)在l
2上是否存在点M,使△ABM是以AB为斜边且一个角为30°的直角三角形?若存在,求出点M的坐标;若不存在,说明理由.
查看答案和解析>>
科目:
来源:第34章《二次函数》中考题集(43):34.4 二次函数的应用(解析版)
题型:解答题
如图,二次函数y=ax
2的图象与一次函数y=x+b的图象相交于A(-2,2)、B两点,从点A和点B分别引平行于y轴的直线与x轴分别交于C,D两点,点P(t,0),为线段CD上的动点,过点P且平行于y轴的直线与抛物线和直线分别交于R,S.
(1)求一次函数和二次函数的解析式,并求出点B的坐标;
(2)当SR=2RP时,计算线段SR的长;
(3)若线段BD上有一动点Q且其纵坐标为t+3,问是否存在t的值,使S
△BRQ=15?若存在,求t的值;若不存在,说明理由.
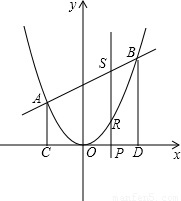
查看答案和解析>>
科目:
来源:第34章《二次函数》中考题集(43):34.4 二次函数的应用(解析版)
题型:解答题
已知抛物线y=ax
2+bx+c经过P(
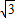
,3),E(
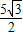
,0)及原点O(0,0).
(1)求抛物线的解析式;
(2)过P点作平行于x轴的直线PC交y轴于C点,在抛物线对称轴右侧且位于直线PC下方的抛物线上,任取一点Q,过点Q作直线QA平行于y轴交x轴于A点,交直线PC于B点,直线QA与直线PC及两坐标轴围成矩形OABC(如图).是否存在点Q,使得△OPC与△PQB相似?若存在,求出Q点的坐标;若不存在,请说明理由;
(3)如果符合(2)中的Q点在x轴的上方,连接OQ,矩形OABC内的四个三角形△OPC,△PQB,△OQP,△OQA之间存在怎样的关系,为什么?
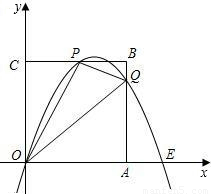
查看答案和解析>>
科目:
来源:第34章《二次函数》中考题集(43):34.4 二次函数的应用(解析版)
题型:解答题
已知抛物线y=ax2+x+2.
(1)当a=-1时,求此抛物线的顶点坐标和对称轴;
(2)若代数式-x2+x+2的值为正整数,求x的值;
(3)当a=a1时,抛物线y=ax2+x+2与x轴的正半轴相交于点M(m,0);当a=a2时,抛物线y=ax2+x+2与x轴的正半轴相交于点N(n,0).若点M在点N的左边,试比较a1与a2的大小.
查看答案和解析>>
科目:
来源:第34章《二次函数》中考题集(44):34.4 二次函数的应用(解析版)
题型:解答题
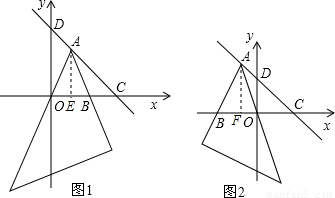
如图1,直线y=-x+1与x轴、y轴分别相交于点C、D,一个含45°角的直角三角板的锐角顶点A在线段CD上滑动,滑动过程中三角板的斜边始终经过坐标原点,∠A的另一边与轴的正半轴相交于点B.
(1)试探索△AOB能否构成以AO、AB为腰的等腰三角形?若能,请求出点B的坐标;若不能,说说明理由;
(2)若将题中“直线y=-x+1”、“∠A的另一边与轴的正半轴相交于点B”分别改为“直线y=-x+t(t>0)”、“∠A的另一边与轴的负半轴相交于点B”(如图2),其他条件不变,试探索△AOB能否为等腰三角形(只考虑点A在线段CD的延长线上且不包括点D时的情况)?若能,请求出点B的坐标;若不能,请说明理由.
查看答案和解析>>
科目:
来源:第34章《二次函数》中考题集(44):34.4 二次函数的应用(解析版)
题型:解答题
如图,一元二次方程x
2+2x-3=0的二根x
1,x
2(x
1<x
2)是抛物线y=ax
2+bx+c与x轴的两个交点B,C的横坐标,且此抛物线过点A(3,6).
(1)求此二次函数的解析式;
(2)设此抛物线的顶点为P,对称轴与线段AC相交于点Q,求点P和点Q的坐标;
(3)在x轴上有一动点M,当MQ+MA取得最小值时,求M点的坐标.
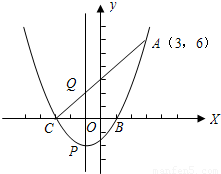
查看答案和解析>>


 ,顶点为P.
,顶点为P.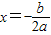 ,顶点坐标是
,顶点坐标是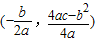 .
.




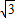 ,3),E(
,3),E(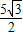 ,0)及原点O(0,0).
,0)及原点O(0,0).