
科目: 来源:第34章《二次函数》中考题集(42):34.4 二次函数的应用(解析版) 题型:解答题
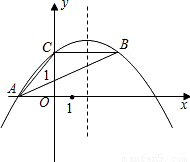 如图,抛物线y=ax2-5ax+4经过△ABC的三个顶点,已知BC∥x轴,点A在x轴上,点C在y轴上,且AC=BC.
如图,抛物线y=ax2-5ax+4经过△ABC的三个顶点,已知BC∥x轴,点A在x轴上,点C在y轴上,且AC=BC.查看答案和解析>>
科目: 来源:第34章《二次函数》中考题集(42):34.4 二次函数的应用(解析版) 题型:解答题
查看答案和解析>>
科目: 来源:第34章《二次函数》中考题集(42):34.4 二次函数的应用(解析版) 题型:解答题
查看答案和解析>>
科目: 来源:第34章《二次函数》中考题集(42):34.4 二次函数的应用(解析版) 题型:解答题
查看答案和解析>>
科目: 来源:第34章《二次函数》中考题集(42):34.4 二次函数的应用(解析版) 题型:解答题
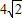 和
和 ,它们的中心O1,O2都在直线l上,AD∥l,EG在直线l上,l与DC相交于点M,ME=7-2
,它们的中心O1,O2都在直线l上,AD∥l,EG在直线l上,l与DC相交于点M,ME=7-2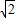 ,当正方形EFGH沿直线l以每秒1个单位的速度向左平移时,正方形ABCD也绕O1以每秒45°顺时针方向开始旋转,在运动变化过程中,它们的形状和大小都不改变.
,当正方形EFGH沿直线l以每秒1个单位的速度向左平移时,正方形ABCD也绕O1以每秒45°顺时针方向开始旋转,在运动变化过程中,它们的形状和大小都不改变.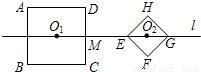
查看答案和解析>>
科目: 来源:第34章《二次函数》中考题集(42):34.4 二次函数的应用(解析版) 题型:解答题
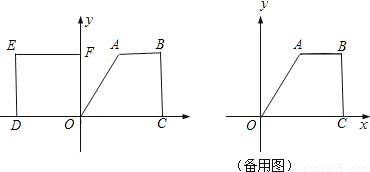
查看答案和解析>>
科目: 来源:第34章《二次函数》中考题集(42):34.4 二次函数的应用(解析版) 题型:解答题
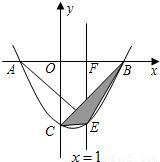
查看答案和解析>>
科目: 来源:第34章《二次函数》中考题集(42):34.4 二次函数的应用(解析版) 题型:解答题
 <x<4时,(3)小题中平行四边形的面积是否有最大值?若有,请求出;若无,请说明理由.
<x<4时,(3)小题中平行四边形的面积是否有最大值?若有,请求出;若无,请说明理由.查看答案和解析>>
科目: 来源:第34章《二次函数》中考题集(43):34.4 二次函数的应用(解析版) 题型:解答题
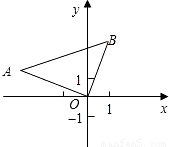
查看答案和解析>>
科目: 来源:第34章《二次函数》中考题集(43):34.4 二次函数的应用(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com