相关习题
0 126507 126515 126521 126525 126531 126533 126537 126543 126545 126551 126557 126561 126563 126567 126573 126575 126581 126585 126587 126591 126593 126597 126599 126601 126602 126603 126605 126606 126607 126609 126611 126615 126617 126621 126623 126627 126633 126635 126641 126645 126647 126651 126657 126663 126665 126671 126675 126677 126683 126687 126693 126701 366461
科目：
来源：第34章《二次函数》中考题集（27）：34.4 二次函数的应用（解析版）
题型：解答题
近几年，被称为“园林城市，生态家园”的宿迁旅游业得到长足的发展，到宿迁观光旅游的客人越来越多，“真如禅寺”景点每天都吸引大量的游客前来观光．事实表明，如果游客过多，不利于保护珍贵文物，为了实施可持续发展，兼顾社会效益和经济效益，该景点拟采取浮动门票价格的方法来控制游客人数．已知每张门票原价为40元，现设浮动门票为每张x元，且40≤x≤70，经市场调研发现一天游览人数y与票价x之间存在着如图所示的一次函数关系．
（1）根据图象，求y与x之间的函数关系式；
（2）设该景点一天的门票收入为W元．
①试用x代数式表示W；
②试问：当门票定为多少时，该景点一天的门票收入最高？最高门票收入是多少？
查看答案和解析>>
科目：
来源：第34章《二次函数》中考题集（27）：34.4 二次函数的应用（解析版）
题型：解答题
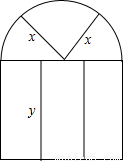
某建筑物的窗户如图所示，它的上半部是半圆，下半部是矩形，制造窗框的材料总长（图中所有黑线的长度和）为10米．当x等于多少米时，窗户的透光面积最大，最大面积是多少？
查看答案和解析>>
科目：
来源：第34章《二次函数》中考题集（27）：34.4 二次函数的应用（解析版）
题型：解答题
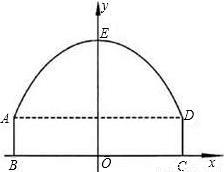
如图，隧道的截面由抛物线AED和矩形ABCD构成，矩形的长BC为8m，宽AB为2m，以BC所在的直线为x轴，线段BC的中垂线为y轴，建立平面直角坐标系．y轴是抛物线的对称轴，顶点E到坐标原点O的距离为6m．
（1）求抛物线的解析式；
（2）如果该隧道内设双行道，现有一辆货运卡车高4.2m，宽2.4米，这辆货运卡车能否通过该隧道？通过计算说明你的结论．
查看答案和解析>>
科目：
来源：第34章《二次函数》中考题集（27）：34.4 二次函数的应用（解析版）
题型：解答题
某化工厂材料经销公司购进了一种化工原料共7000千克，购进价格为每千克30元，物价部门规定其销售单价不得高于每千克70元，也不得低于每千克30元．市场调查发现；单价定为70元时，每日平均销售60千克；单价每降低1元，每日平均多售出2千克．在销售过程中，每天还要支出其它费用500元（天数不足1天时按整天计算）．
（1）每日平均销售可以表示为______；
（2）每日平均销售额可以表示为______；
（3）每日平均获利可以表示为y=______；
（4）当销售单价是______元时，每日平均获利最多，是______元；
（5）若将这种化工原料全部售出，比较每日平均获利最多和销售单价最高这两种销售方式．哪一种获总利润最多？
查看答案和解析>>
科目：
来源：第34章《二次函数》中考题集（27）：34.4 二次函数的应用（解析版）
题型：解答题
某工厂生产的某种产品按质量分为10个档次，生产第一档次（即最低档次）的产品一天生产76件，每件利润10元，每提高一个档次，利润每件增加2元．
（1）每件利润为16元时，此产品质量在第几档次？
（2）由于生产工序不同，此产品每提高一个档次，一天产量减少4件．若生产第x档的产品一天的总利润为y元（其中x为正整数，且1≤x≤10），求出y关于x的函数关系式；若生产某档次产品一天的总利润为1080元，该工厂生产的是第几档次的产品？
查看答案和解析>>
科目：
来源：第34章《二次函数》中考题集（27）：34.4 二次函数的应用（解析版）
题型：解答题
现有铝合金窗框料8米，准备用它做一个如图所示的长方形窗架，一般来说，当窗户总面积最大时，窗户的透光最好．那么，要使这个窗户透光最好，窗架的宽应为多少米此时窗户的总面积是多少平方米？
查看答案和解析>>
科目：
来源：第34章《二次函数》中考题集（27）：34.4 二次函数的应用（解析版）
题型：解答题
如图是泰州某河上一座古拱桥的截面图，拱桥桥洞上沿是抛物线形状，抛物线两端点与水面的距离都是1m，拱桥的跨度为10m，桥洞与水面的最大距离是5m，桥洞两侧壁上各有一盏距离水面4m的景观灯．若把拱桥的截面图放在平面直角坐标系中（如图）．
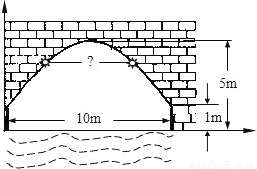
（1）求抛物线的解析式；（2）求两盏景观灯之间的水平距离．
查看答案和解析>>
科目：
来源：第34章《二次函数》中考题集（27）：34.4 二次函数的应用（解析版）
题型：解答题
如图，用长为18 m的篱笆（虚线部分），两面靠墙围成矩形的苗圃．
（1）设矩形的一边为x（m），面积为y（m
2），求y关于x的函数关系式，并写出自变量x的取值范围；
（2）当x为何值时，所围苗圃的面积最大，最大面积是多少？
查看答案和解析>>
科目：
来源：第34章《二次函数》中考题集（27）：34.4 二次函数的应用（解析版）
题型：解答题
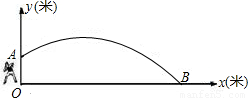
如图，一个中学生推铅球，铅球在点A处出手，在点B处落地，它的运行路线是一条抛物线，在平面直角坐标系中，这条抛物线的解析式为：y=
x
2+
x+
（1）请用配方法把y=-
x
2+
x+
化成y=a（x-h）
2+k的形式．
（2）求出铅球在运行过程中到达最高点时离地面的距离和这个学生推铅球的成绩．（单位：米）
查看答案和解析>>
科目：
来源：第34章《二次函数》中考题集（28）：34.4 二次函数的应用（解析版）
题型：解答题
农民张大伯为了致富奔小康，大力发展家庭养殖业．他准备用40m长的木栏围一个矩形的羊圈，为了节约材料同时要使矩形的面积最大，他利用了自家房屋一面长25m的墙，设计了如图一个矩形的羊圈．
（1）请你求出张大伯矩形羊圈的面积；
（2）请你判断他的设计方案是否合理？如果合理，直接答合理；如果不合理又该如何设计并说明理由．
查看答案和解析>>
