
科目: 来源:第34章《二次函数》中考题集(25):34.4 二次函数的应用(解析版) 题型:解答题
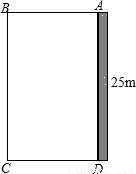
查看答案和解析>>
科目: 来源:第34章《二次函数》中考题集(25):34.4 二次函数的应用(解析版) 题型:解答题
 ,为充分利用土地资源,更好地解决人们的住房需求,并适当的控制建筑物的高度,一般地容积率t不小于1且不大于8.一房地产开发商在开发某小区时,结合往年开发经验知,建筑面积M(m2)与容积率t的关系可近似地用如图(1)中的线段l来表示;1 m2建筑面积上的资金投入Q(万元)与容积率t的关系可近似地用如图(2)中的一段抛物线段c来表示.
,为充分利用土地资源,更好地解决人们的住房需求,并适当的控制建筑物的高度,一般地容积率t不小于1且不大于8.一房地产开发商在开发某小区时,结合往年开发经验知,建筑面积M(m2)与容积率t的关系可近似地用如图(1)中的线段l来表示;1 m2建筑面积上的资金投入Q(万元)与容积率t的关系可近似地用如图(2)中的一段抛物线段c来表示.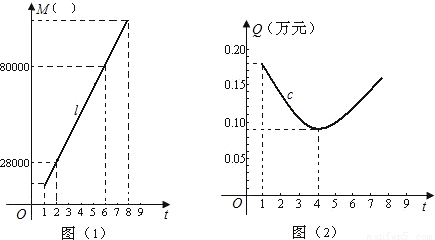
查看答案和解析>>
科目: 来源:第34章《二次函数》中考题集(25):34.4 二次函数的应用(解析版) 题型:解答题

查看答案和解析>>
科目: 来源:第34章《二次函数》中考题集(25):34.4 二次函数的应用(解析版) 题型:解答题

查看答案和解析>>
科目: 来源:第34章《二次函数》中考题集(25):34.4 二次函数的应用(解析版) 题型:解答题
查看答案和解析>>
科目: 来源:第34章《二次函数》中考题集(25):34.4 二次函数的应用(解析版) 题型:解答题
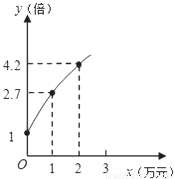
查看答案和解析>>
科目: 来源:第34章《二次函数》中考题集(25):34.4 二次函数的应用(解析版) 题型:解答题
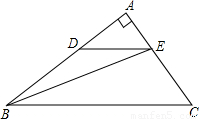
查看答案和解析>>
科目: 来源:第34章《二次函数》中考题集(25):34.4 二次函数的应用(解析版) 题型:解答题
查看答案和解析>>
科目: 来源:第34章《二次函数》中考题集(25):34.4 二次函数的应用(解析版) 题型:解答题

查看答案和解析>>
科目: 来源:第34章《二次函数》中考题集(27):34.4 二次函数的应用(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com