相关习题
0 126519 126527 126533 126537 126543 126545 126549 126555 126557 126563 126569 126573 126575 126579 126585 126587 126593 126597 126599 126603 126605 126609 126611 126613 126614 126615 126617 126618 126619 126621 126623 126627 126629 126633 126635 126639 126645 126647 126653 126657 126659 126663 126669 126675 126677 126683 126687 126689 126695 126699 126705 126713 366461
科目:
来源:第34章《二次函数》中考题集(22):34.4 二次函数的应用(解析版)
题型:解答题
如图,小明在一次高尔夫球争霸赛中,从山坡下O点打出一球向球洞A点飞去,球的飞行路线为抛物线,如果不考虑空气阻力,当球达到最大水平高度12米时,球移动的水平距离为9米.已知山坡OA与水平方向OC的夹角为30°,O、A两点相距8
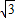
米.
(1)求出点A的坐标及直线OA的解析式;
(2)求出球的飞行路线所在抛物线的解析式;
(3)判断小明这一杆能否把高尔夫球从O点直接打入球洞A点?
查看答案和解析>>
科目:
来源:第34章《二次函数》中考题集(22):34.4 二次函数的应用(解析版)
题型:解答题
某水果批发商场经销一种高档水果,如果每千克盈利10元,每天可售出500千克.经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克.
(1)现该商场要保证每天盈利6 000元,同时又要顾客得到实惠,那么每千克应涨价多少元?
(2)若该商场单纯从经济角度看,每千克这种水果涨价多少元,能使商场获利最多?
查看答案和解析>>
科目:
来源:第34章《二次函数》中考题集(22):34.4 二次函数的应用(解析版)
题型:解答题
某市政府大力扶持大学生创业,李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:y=-10x+500.
(1)设李明每月获得利润为w(元),当销售单价定为多少元时,每月可获得最大利润?
(2)如果李明想要每月获得2000元的利润,那么销售单价应定为多少元?
(3)根据物价部门规定,这种护眼台灯的销售单价不得高于32元,如果李明想要每月获得的利润不低于2000元,那么他每月的成本最少需要多少元?
(成本=进价×销售量)
查看答案和解析>>
科目:
来源:第34章《二次函数》中考题集(22):34.4 二次函数的应用(解析版)
题型:解答题
如图,在水平地面点A处有一网球发射器向空中发射网球,网球飞行路线是一条抛物线,在地面上落点为B.有人在直线AB上点C(靠点B一侧)竖直向上摆放无盖的圆柱形桶,试图让网球落入桶内.已知AB=4米,AC=3米,网球飞行最大高度OM=5米,圆柱形桶的直径为0.5米,高为0.3米(网球的体积和圆柱形桶的厚度忽略不计).
(1)如果竖直摆放5个圆柱形桶时,网球能不能落入桶内?
(2)当竖直摆放圆柱形桶多少个时,网球可以落入桶内?
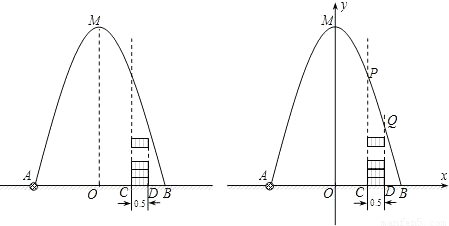
查看答案和解析>>
科目:
来源:第34章《二次函数》中考题集(22):34.4 二次函数的应用(解析版)
题型:解答题
如图,八一广场要设计一个矩形花坛,花坛的长、宽分别为200m、120m,花坛中有一横两纵的通道,横、纵通道的宽度分别为3xm、2xm.
(1)用代数式表示三条通道的总面积S;当通道总面积为花坛总面积的

时,求横、纵通道的宽分别是多少?
(2)如果花坛绿化造价为每平方米3元,通道总造价为3168x元,那么横、纵通道的宽分别为多少米时,花坛总造价最低?并求出最低造价.
(以下数据可供参考:85
2=7225,86
2=7396,87
2=7569)
查看答案和解析>>
科目:
来源:第34章《二次函数》中考题集(22):34.4 二次函数的应用(解析版)
题型:解答题
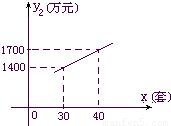
国家推行“节能减排,低碳经济”政策后,某环保节能设备生产企业的产品供不应求.若该企业的某种环保设备每月的产量保持在一定的范围,每套产品的生产成本不高于50万元,每套产品的售价不低于90万元.已知这种设备的月产量x(套)与每套的售价y
1(万元)之间满足关系式y
1=170-2x,月产量x(套)与生产总成本y
2(万元)存在如图所示的函数关系.
(1)直接写出y
2与x之间的函数关系式;
(2)求月产量x的范围;
(3)当月产量x(套)为多少时,这种设备的利润W(万元)最大?最大利润是多少?
查看答案和解析>>
科目:
来源:第34章《二次函数》中考题集(22):34.4 二次函数的应用(解析版)
题型:解答题
某商店经营一种小商品,进价为2.5元,据市场调查,销售单价是13.5元时平均每天销售量是500件,而销售价每降低1元,平均每天就可以多售出100件.
(1)假定每件商品降价x元,商店每天销售这种小商品的利润是y元,请写出y与x间的函数关系式,并注明x的取值范围.
(2)每件小商品销售价是多少元时,商店每天销售这种小商品的利润最大?最大利润是多少?(注:销售利润=销售收入-购进成本)
查看答案和解析>>
科目:
来源:第34章《二次函数》中考题集(22):34.4 二次函数的应用(解析版)
题型:解答题
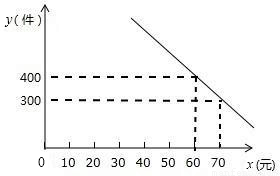
某商场购进一批单价为50元的商品,规定销售时单价不低于进价,每件的利润不超过40%.其中销售量y(件)与所售单价x(元)的关系可以近似的看作如图所表示的一次函数.
(1)求y与x之间的函数关系式,并求出x的取值范围;
(2)设该公司获得的总利润(总利润=总销售额-总成本)为w元,求w与x之间的函数关系式,当销售单价为何值时,所获利润最大,最大利润是多少?
查看答案和解析>>
科目:
来源:第34章《二次函数》中考题集(22):34.4 二次函数的应用(解析版)
题型:解答题
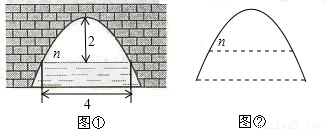
如图中是抛物线形拱桥,当水面在n时,拱顶离水面2m,水面宽4m,水面下降1m,水面宽度增加多少?
查看答案和解析>>
科目:
来源:第34章《二次函数》中考题集(22):34.4 二次函数的应用(解析版)
题型:解答题
如图,东梅中学要在教学楼后面的空地上用40米长的竹篱笆围出一个矩形地块作生物园,矩形的一边用教学楼的外墙,其余三边用竹篱笆.设矩形的宽为x,面积为y.
(1)求y与x的函数关系式,并求自变量x的取值范围;
(2)生物园的面积能否达到210平方米?说明理由.

查看答案和解析>>

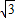 米.
米.

 时,求横、纵通道的宽分别是多少?
时,求横、纵通道的宽分别是多少?



