
科目: 来源:第34章《二次函数》中考题集(22):34.4 二次函数的应用(解析版) 题型:解答题
| 周数x | 1 | 2 | 3 | 4 |
| 价格y(元/kg) | 2 | 2.2 | 2.4 | 2.6 |
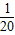 x2+bx+c.
x2+bx+c. x+1.2,5月份此种蔬菜的进价m(元/千克)与周数x所满足的函数关系为m=
x+1.2,5月份此种蔬菜的进价m(元/千克)与周数x所满足的函数关系为m=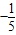 x+2.试问4月份与5月份分别在哪一周销售此种蔬菜一千克的利润最大?且最大利润分别是多少?
x+2.试问4月份与5月份分别在哪一周销售此种蔬菜一千克的利润最大?且最大利润分别是多少?查看答案和解析>>
科目: 来源:第34章《二次函数》中考题集(22):34.4 二次函数的应用(解析版) 题型:解答题
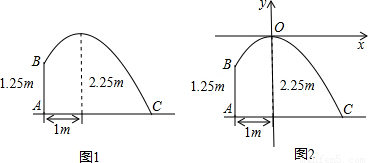
查看答案和解析>>
科目: 来源:第34章《二次函数》中考题集(22):34.4 二次函数的应用(解析版) 题型:解答题
| 车厢节数n | 4 | 7 | 10 |
| 往返次数m | 16 | 10 | 4 |
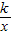 (k为常数,k≠0)③y=ax2+bx+c(a,b,c为常数,a≠0)中,选取一个合适的函数模型,求出的m关于n的函数关系式是m=______(不写n的取值范围);
(k为常数,k≠0)③y=ax2+bx+c(a,b,c为常数,a≠0)中,选取一个合适的函数模型,求出的m关于n的函数关系式是m=______(不写n的取值范围);查看答案和解析>>
科目: 来源:第34章《二次函数》中考题集(22):34.4 二次函数的应用(解析版) 题型:解答题
查看答案和解析>>
科目: 来源:第34章《二次函数》中考题集(22):34.4 二次函数的应用(解析版) 题型:解答题
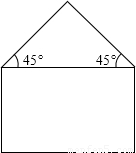
查看答案和解析>>
科目: 来源:第34章《二次函数》中考题集(22):34.4 二次函数的应用(解析版) 题型:解答题

查看答案和解析>>
科目: 来源:第34章《二次函数》中考题集(22):34.4 二次函数的应用(解析版) 题型:解答题
查看答案和解析>>
科目: 来源:第34章《二次函数》中考题集(22):34.4 二次函数的应用(解析版) 题型:解答题
查看答案和解析>>
科目: 来源:第34章《二次函数》中考题集(22):34.4 二次函数的应用(解析版) 题型:解答题
| 项目 百分比 种植基地 | 该基地的累积产量占两基地累积总产量的百分比 | 该基地累积存入仓库的量占该基地的累积产量的百分比 |
| 甲 | 60% | 85% |
| 乙 | 40% | 22.5% |
查看答案和解析>>
科目: 来源:第34章《二次函数》中考题集(22):34.4 二次函数的应用(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com