相关习题
0 126954 126962 126968 126972 126978 126980 126984 126990 126992 126998 127004 127008 127010 127014 127020 127022 127028 127032 127034 127038 127040 127044 127046 127048 127049 127050 127052 127053 127054 127056 127058 127062 127064 127068 127070 127074 127080 127082 127088 127092 127094 127098 127104 127110 127112 127118 127122 127124 127130 127134 127140 127148 366461
科目:
来源:第2章《二次函数》常考题集(23):2.3 二次函数的应用(解析版)
题型:解答题
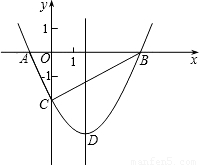
如图,抛物线y=

x
2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M(m,0)是x轴上的一个动点,当MC+MD的值最小时,求m的值.
[注:抛物线y=ax
2+bx+c的顶点坐标为(-
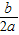
,
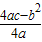
).].
查看答案和解析>>
科目:
来源:第2章《二次函数》常考题集(23):2.3 二次函数的应用(解析版)
题型:解答题
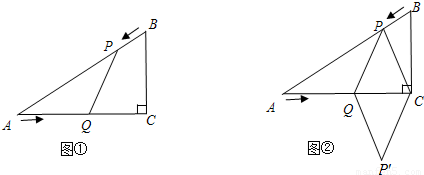
已知:如图①,在Rt△ACB中,∠C=90°,AC=4 cm,BC=3 cm,点P由B出发沿BA方向向点A匀速运动,速度为1cm/s;点Q由A出发沿AC方向向点C匀速运动,速度为2cm/s;连接PQ.若设运动的时间为t(s)(0<t<2),解答下列问题:
(1)当t为何值时,PQ∥BC;
(2)设△AQP的面积为y(cm
2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使线段PQ恰好把Rt△ACB的周长和面积同时平分?若存在,求出此时t的值;若不存在,说明理由;
(4)如图②,连接PC,并把△PQC沿QC翻折,得到四边形PQP′C,那么是否存在某一时刻t,使四边形PQP′C为菱形?若存在,求出此时菱形的边长;若不存在,说明理由.
查看答案和解析>>
科目:
来源:第2章《二次函数》常考题集(23):2.3 二次函数的应用(解析版)
题型:解答题
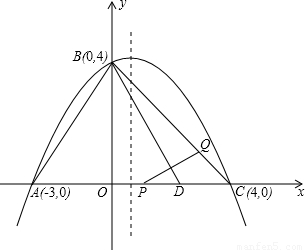
如图:抛物线经过A(-3,0)、B(0,4)、C(4,0)三点.
(1)求抛物线的解析式.
(2)已知AD=AB(D在线段AC上),有一动点P从点A沿线段AC以每秒1个单位长度的速度移动;同时另一个动点Q以某一速度从点B沿线段BC移动,经过t秒的移动,线段PQ被BD垂直平分,求t的值;
(3)在(2)的情况下,抛物线的对称轴上是否存在一点M,使MQ+MC有最小值?若存在,请求出点M的坐标;若不存在,请说明理由.(注:抛物线y=ax
2+bx+c的对称轴为x=-
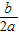
)
查看答案和解析>>
科目:
来源:第2章《二次函数》常考题集(23):2.3 二次函数的应用(解析版)
题型:解答题
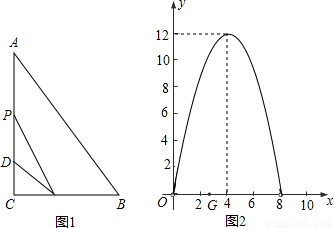
如图1,在Rt△ABC中,∠C=90°,BC=8厘米,点D在AC上,CD=3厘米.点P、Q分别由A、C两点同时出发,点P沿AC方向向点C匀速移动,速度为每秒k厘米,行完AC全程用时8秒;点Q沿CB方向向点B匀速移动,速度为每秒1厘米.设运动的时间为x秒(0<x<8),△DCQ的面积为y
1平方厘米,△PCQ的面积为y
2平方厘米.
(1)求y
1与x的函数关系,并在图2中画出y
1的图象;
(2)如图2,y
2的图象是抛物线的一部分,其顶点坐标是(4,12),求点P的速度及AC的长;
(3)在图2中,点G是x轴正半轴上一点0<OG<6,过G作EF垂直于x轴,分别交y
1、y
2的图象于点E、F.
①说出线段EF的长在图1中所表示的实际意义;
②当0<x<6时,求线段EF长的最大值.
查看答案和解析>>
科目:
来源:第2章《二次函数》常考题集(23):2.3 二次函数的应用(解析版)
题型:解答题
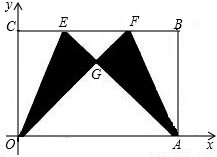
如图,平面直角坐标系中有一矩形纸片OABC,O为原点,点A,C分别在x轴,y轴上,点B坐标为(m,
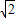
)(其中m>0),在BC边上选取适当的点E和点F,将△OCE沿OE翻折,得到△OGE;再将△ABF沿AF翻折,恰好使点B与点G重合,得到△AGF,且∠OGA=90度.
(1)求m的值;
(2)求过点O,G,A的抛物线的解析式和对称轴;
(3)在抛物线的对称轴上是否存在点P,使得△OPG是等腰三角形?若不存在,请说明理由;若存在,直接答出所有满足条件的点P的坐标(不要求写出求解过程).
查看答案和解析>>
科目:
来源:第2章《二次函数》常考题集(23):2.3 二次函数的应用(解析版)
题型:解答题
如图,已知平面直角坐标系xoy中,有一矩形纸片OABC,O为坐标原点,AB∥x轴,B(3,
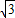
),现将纸片按如图折叠,AD,DE为折痕,∠OAD=30度.折叠后,点O落在点O
1,点C落在线段AB点C
1处,并且DO
1与DC
1在同一直线上.
(1)求折痕AD所在直线的解析式;
(2)求经过三点O,C
1,C的抛物线的解析式;
(3)若⊙P的半径为R,圆心P在(2)的抛物线上运动,⊙P与两坐标轴都相切时,求⊙P半径R的值.
查看答案和解析>>
科目:
来源:第2章《二次函数》常考题集(23):2.3 二次函数的应用(解析版)
题型:解答题
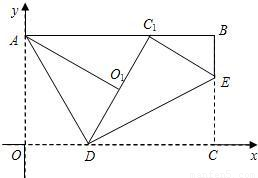
如图,抛物线y
1=-ax
2-ax+1经过点P(-

,

),且与抛物线y
2=ax
2-ax-1相交于A,B两点.
(1)求a值;
(2)设y
1=-ax
2-ax+1与x轴分别交于M,N两点(点M在点N的左边),y
2=ax
2-ax-1与x轴分别交于E,F两点(点E在点F的左边),观察M,N,E,F四点的坐标,写出一条正确的结论,并通过计算说明;
(3)设A,B两点的横坐标分别记为x
A,x
B,若在x轴上有一动点Q(x,0),且x
A≤x≤x
B,过Q作一条垂直于x轴的直线,与两条抛物线分别交于C,D两点,试问当x为何值时,线段CD有最大值,其最大值为多少?
查看答案和解析>>
科目:
来源:第2章《二次函数》常考题集(23):2.3 二次函数的应用(解析版)
题型:解答题
如图所示,E是正方形ABCD的边AB上的动点,EF⊥DE交BC于点F.
(1)求证:△ADE∽△BEF;
(2)设正方形的边长为4,AE=x,BF=y.当x取什么值时,y有最大值?并求出这个最大值.

查看答案和解析>>
科目:
来源:第2章《二次函数》常考题集(23):2.3 二次函数的应用(解析版)
题型:解答题
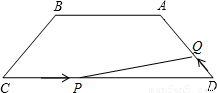
如图,等腰梯形ABCD中,AB=4,CD=9,∠C=60°,动点P从点C出发沿CD方向向点D运动,动点Q同时以相同速度从点D出发沿DA方向向终点A运动,其中一个动点到达端点时,另一个动点也随之停止运动.
(1)求AD的长;
(2)设CP=x,问当x为何值时△PDQ的面积达到最大,并求出最大值;
(3)探究:在BC边上是否存在点M使得四边形PDQM是菱形?若存在,请找出点M,并求出BM的长;不存在,请说明理由.
查看答案和解析>>
科目:
来源:第2章《二次函数》常考题集(23):2.3 二次函数的应用(解析版)
题型:解答题
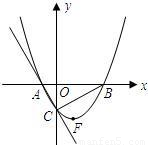
如图,在平面直角坐标系中,直线y=-
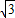
x-
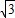
与x轴交于点A,与y轴交于点C,抛物线y=ax
2-
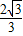
x+c(a≠0)经过A,B,C三点.
(1)求过A,B,C三点抛物线的解析式并求出顶点F的坐标;
(2)在抛物线上是否存在点P,使△ABP为直角三角形?若存在,直接写出P点坐标;若不存在,请说明理由;
(3)试探究在直线AC上是否存在一点M,使得△MBF的周长最小?若存在,求出M点的坐标;若不存在,请说明理由.
查看答案和解析>>

 x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0).
x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0).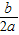 ,
,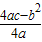 ).].
).].

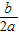 )
)

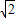 )(其中m>0),在BC边上选取适当的点E和点F,将△OCE沿OE翻折,得到△OGE;再将△ABF沿AF翻折,恰好使点B与点G重合,得到△AGF,且∠OGA=90度.
)(其中m>0),在BC边上选取适当的点E和点F,将△OCE沿OE翻折,得到△OGE;再将△ABF沿AF翻折,恰好使点B与点G重合,得到△AGF,且∠OGA=90度.
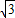 ),现将纸片按如图折叠,AD,DE为折痕,∠OAD=30度.折叠后,点O落在点O1,点C落在线段AB点C1处,并且DO1与DC1在同一直线上.
),现将纸片按如图折叠,AD,DE为折痕,∠OAD=30度.折叠后,点O落在点O1,点C落在线段AB点C1处,并且DO1与DC1在同一直线上.
 ,
, ),且与抛物线y2=ax2-ax-1相交于A,B两点.
),且与抛物线y2=ax2-ax-1相交于A,B两点.


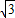 x-
x-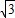 与x轴交于点A,与y轴交于点C,抛物线y=ax2-
与x轴交于点A,与y轴交于点C,抛物线y=ax2-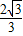 x+c(a≠0)经过A,B,C三点.
x+c(a≠0)经过A,B,C三点.