相关习题
0 126965 126973 126979 126983 126989 126991 126995 127001 127003 127009 127015 127019 127021 127025 127031 127033 127039 127043 127045 127049 127051 127055 127057 127059 127060 127061 127063 127064 127065 127067 127069 127073 127075 127079 127081 127085 127091 127093 127099 127103 127105 127109 127115 127121 127123 127129 127133 127135 127141 127145 127151 127159 366461
科目：
来源：第2章《二次函数》常考题集（17）：2.3 二次函数的应用（解析版）
题型：解答题
已知二次函数y=x2+bx+c的图象与x轴的两个交点的横坐标分别为x1、x2，一元二次方程x2+b2x+20=0的两实根为x3、x4，且x2-x3=x1-x4=3，求二次函数的解析式，并写出顶点坐标．
查看答案和解析>>
科目：
来源：第2章《二次函数》常考题集（17）：2.3 二次函数的应用（解析版）
题型：解答题
利用图象解一元二次方程x
2+x-3=0时，我们采用的一种方法是：在平面直角坐标系中画出抛物线y=x
2和直线y=-x+3，两图象交点的横坐标就是该方程的解．
（1）填空：利用图象解一元二次方程x
2+x-3=0，也可以这样求解：在平面直角坐标系中画出抛物线y=______和直线y=-x，其交点的横坐标就是该方程的解．
（2）已知函数y=-
的图象（如图所示），利用图象求方程
-x+3=0的近似解．（结果保留两个有效数字）
查看答案和解析>>
科目：
来源：第2章《二次函数》常考题集（17）：2.3 二次函数的应用（解析版）
题型：解答题
小明在复习数学知识时，针对“求一元二次方程的解”，整理了以下的几种方法，请你按有关内容补充完整：
| 复习日记卡片 |
| 内容：一元二次方程解法归纳 时间：2007年6月×日 |
| 举例：求一元二次方程x2-x-1=0的两个解 |
方法一：选择合适的一种方法（公式法、配方法、分解因式法）求解
解方程：x2-x-1=0．
解： |
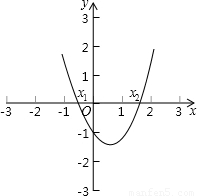
方法二：利用二次函数图象与坐标轴的交点求解如图所示，把方程x2-x-1=0的解看成是二次函数y=______的图象与x轴交点的横坐标，即x1，x2就是方程的解．
 |
方法三：利用两个函数图象的交点求解
（1）把方程x2-x-1=0的解看成是一个二次函数y=______的图象与一个一次函数y=______图象交点的横坐标；
（2）画出这两个函数的图象，用x1，x2在x轴上标出方程的解．
 |
查看答案和解析>>
科目：
来源：第2章《二次函数》常考题集（17）：2.3 二次函数的应用（解析版）
题型：解答题
利用二次函数的图象求下列一元二次方程的近似根．
（1）x2-2x-1=0；（2）x2+5=4x．
查看答案和解析>>
科目：
来源：第2章《二次函数》常考题集（17）：2.3 二次函数的应用（解析版）
题型：解答题
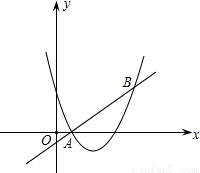
如图，直线y=x+m和抛物线y=x
2+bx+c都经过点A（1，0），B（3，2）．
（1）求m的值和抛物线的解析式；
（2）求不等式x
2+bx+c＞x+m的解集．（直接写出答案）
查看答案和解析>>
科目：
来源：第2章《二次函数》常考题集（17）：2.3 二次函数的应用（解析版）
题型：解答题
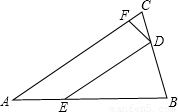
如图，在△ABC中，AB=AC，点D在BC上，DE∥AC，交AB与点E，点F在AC上，DC=DF，若BC=3，EB=4，CD=x，CF=y，求y与x的函数关系式，并写出自变量x的取值范围．
查看答案和解析>>
科目：
来源：第2章《二次函数》常考题集（17）：2.3 二次函数的应用（解析版）
题型：解答题
某公司经销一种绿茶，每千克成本为50元．市场调查发现，在一段时间内，销售量w（千克）随销售单价x（元/千克）的变化而变化，具体关系式为：w=-2x+240．设这种绿茶在这段时间内的销售利润为y（元），解答下列问题：
（1）求y与x的关系式；
（2）当x取何值时，y的值最大？
（3）如果物价部门规定这种绿茶的销售单价不得高于90元/千克，公司想要在这段时间内获得2250元的销售利润，销售单价应定为多少元？
查看答案和解析>>
科目：
来源：第2章《二次函数》常考题集（17）：2.3 二次函数的应用（解析版）
题型：解答题
某水果批发商场经销一种高档水果，如果每千克盈利10元，每天可售出500千克．经市场调查发现，在进货价不变的情况下，若每千克涨价1元，日销售量将减少20千克．
（1）现该商场要保证每天盈利6 000元，同时又要顾客得到实惠，那么每千克应涨价多少元？
（2）若该商场单纯从经济角度看，每千克这种水果涨价多少元，能使商场获利最多？
查看答案和解析>>
科目：
来源：第2章《二次函数》常考题集（17）：2.3 二次函数的应用（解析版）
题型：解答题
荆州市“建设社会主义新农村”工作组到某县大棚蔬菜生产基地指导菜农修建大棚种植蔬菜．通过调查得知：平均修建每公顷大棚要用支架、农膜等材料费2.7万元；购置滴灌设备，这项费用（万元）与大棚面积（公顷）的平方成正比，比例系数为0.9；另外每公顷种植蔬菜需种子、化肥、农药等开支0.3万元．每公顷蔬菜年均可卖7.5万元．
（1）基地的菜农共修建大棚x（公顷），当年收益（扣除修建和种植成本后）为y（万元），写出y关于x的函数关系式．
（2）若某菜农期望通过种植大棚蔬菜当年获得5万元收益，工作组应建议他修建多少公顷大棚．（用分数表示即可）
（3）除种子、化肥、农药投资只能当年受益外，其它设施3年内不需增加投资仍可继续使用．如果按3年计算，是否修建大棚面积越大收益越大？修建面积为多少时可以得到最大收益？请帮工作组为基地修建大棚提一项合理化建议．
查看答案和解析>>
科目：
来源：第2章《二次函数》常考题集（17）：2.3 二次函数的应用（解析版）
题型：解答题
某商场试销一种成本为每件60元的服装，规定试销期间销售单价不低于成本单价，且获利不得高于45%，经试销发现，销售量y（件）与销售单价x（元）符合一次函数y=kx+b，且x=65时，y=55；x=75时，y=45．
（1）求一次函数y=kx+b的表达式；
（2）若该商场获得利润为W元，试写出利润W与销售单价x之间的关系式；销售单价定为多少元时，商场可获得最大利润，最大利润是多少元？
（3）若该商场获得利润不低于500元，试确定销售单价x的范围．
查看答案和解析>>
