相关习题
0 126966 126974 126980 126984 126990 126992 126996 127002 127004 127010 127016 127020 127022 127026 127032 127034 127040 127044 127046 127050 127052 127056 127058 127060 127061 127062 127064 127065 127066 127068 127070 127074 127076 127080 127082 127086 127092 127094 127100 127104 127106 127110 127116 127122 127124 127130 127134 127136 127142 127146 127152 127160 366461
科目:
来源:第2章《二次函数》常考题集(17):2.3 二次函数的应用(解析版)
题型:解答题
已知二次函数的图象以A(-1,4)为顶点,且过点B(2,-5)
①求该函数的关系式;
②求该函数图象与坐标轴的交点坐标;
③将该函数图象向右平移,当图象经过原点时,A、B两点随图象移至A′、B′,求△O A′B′的面积.
查看答案和解析>>
科目:
来源:第2章《二次函数》常考题集(17):2.3 二次函数的应用(解析版)
题型:解答题
(1)用配方法把二次函数y=x2-4x+3变成y=(x-h)2+k的形成.
(2)在直角坐标系中画出y=x2-4x+3的图象.
(3)若A(x1,y1),B(x2,y2)是函数y=x2-4x+3图象上的两点,且x1<x2<1,请比较y1,y2的大小关系.(直接写结果)
(4)把方程x2-4x+3=2的根在函数y=x2-4x+3的图象上表示出来.
查看答案和解析>>
科目:
来源:第2章《二次函数》常考题集(17):2.3 二次函数的应用(解析版)
题型:解答题
已知:关于x的一元二次方程mx
2-(3m+2)x+2m+2=0(m>0).
(1)求证:方程有两个不相等的实数根;
(2)设方程的两个实数根分别为x
1,x
2(其中x
1<x
2).若y是关于m的函数,且y=x
2-2x
1,求这个函数的解析式;
(3)在(2)的条件下,结合函数的图象回答:当自变量m的取值范围满足什么条件时,y≤2m.
查看答案和解析>>
科目:
来源:第2章《二次函数》常考题集(17):2.3 二次函数的应用(解析版)
题型:解答题
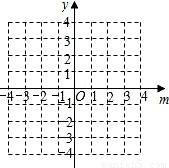
二次函数y=ax
2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:
(1)写出方程ax
2+bx+c=0的两个根;
(2)写出不等式ax
2+bx+c>0的解集;
(3)写出y随x的增大而减小的自变量x的取值范围;
(4)若方程ax
2+bx+c=k有两个不相等的实数根,求k的取值范围.

查看答案和解析>>
科目:
来源:第2章《二次函数》常考题集(17):2.3 二次函数的应用(解析版)
题型:解答题
已知关于x的二次函数y=x
2-mx+
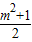
与y=x
2-mx-
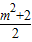
,这两个二次函数的图象中的一条与x轴交于A,B两个不同的点.
(1)试判断哪个二次函数的图象经过A,B两点;
(2)若A点坐标为(-1,0),试求B点坐标;
(3)在(2)的条件下,对于经过A,B两点的二次函数,当x取何值时,y的值随x值的增大而减小.
查看答案和解析>>
科目:
来源:第2章《二次函数》常考题集(17):2.3 二次函数的应用(解析版)
题型:解答题
已知二次函数y=2x2-mx-m2.
(1)求证:对于任意实数m,该二次函数图象与x轴总有公共点;
(2)若该二次函数图象与x轴有两个公共点A,B,且A点坐标为(1,0),求B点坐标.
查看答案和解析>>
科目:
来源:第2章《二次函数》常考题集(17):2.3 二次函数的应用(解析版)
题型:解答题
已知抛物线y=x2-2x-8.
(1)试说明该抛物线与x轴一定有两个交点.
(2)若该抛物线与x轴的两个交点分别为A、B(A在B的左边),且它的顶点为P,求△ABP的面积.
查看答案和解析>>
科目:
来源:第2章《二次函数》常考题集(17):2.3 二次函数的应用(解析版)
题型:解答题
已知:二次函数y=x
2-2(m-1)x+m
2-2m-3,其中m为实数.
(1)求证:不论m取何实数,这个二次函数的图象与x轴必有两个交点;
(2)设这个二次函数的图象与x轴交于点A(x
1,0)、B(x
2,0),且x
1、x
2的倒数和为

,求这个二次函数的解析式.
查看答案和解析>>
科目:
来源:第2章《二次函数》常考题集(17):2.3 二次函数的应用(解析版)
题型:解答题
已知:二次函数y=x
2-mx-4.
(1)求证:该函数的图象一定与x轴有两个不同的交点;
(2)设该函数的图象与x轴的交点坐标为(x
1,0)、(x
2,0),且
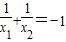
,求m的值,并求出该函数图象的顶点坐标.
查看答案和解析>>
科目:
来源:第2章《二次函数》常考题集(17):2.3 二次函数的应用(解析版)
题型:解答题
一元二次方程x2+2x-3=0的二根x1,x2(x1<x2)是抛物线y=ax2+bx+c与x轴的两个交点B,C的横坐标,且此抛物线过点A(3,6).
(1)求此二次函数的解析式;
(2)用配方法求此抛物线的顶点为P;
(3)当x取什么值时,y随x增大而减小?
查看答案和解析>>



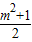 与y=x2-mx-
与y=x2-mx-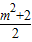 ,这两个二次函数的图象中的一条与x轴交于A,B两个不同的点.
,这两个二次函数的图象中的一条与x轴交于A,B两个不同的点. ,求这个二次函数的解析式.
,求这个二次函数的解析式.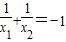 ,求m的值,并求出该函数图象的顶点坐标.
,求m的值,并求出该函数图象的顶点坐标.