相关习题
0 127002 127010 127016 127020 127026 127028 127032 127038 127040 127046 127052 127056 127058 127062 127068 127070 127076 127080 127082 127086 127088 127092 127094 127096 127097 127098 127100 127101 127102 127104 127106 127110 127112 127116 127118 127122 127128 127130 127136 127140 127142 127146 127152 127158 127160 127166 127170 127172 127178 127182 127188 127196 366461
科目:
来源:第2章《二次函数》中考题集(50):2.3 二次函数的应用(解析版)
题型:解答题
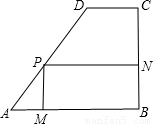
如图,某学校校园内有一块形状为直角梯形的空地ABCD,其中AB∥DC,∠B=90°,AB=100m,BC=80m,CD=40m,现计划在上面建设一个面积为S的矩形综合楼PMBN,其中点P在线段AD上,且PM的长至少为36m.
(1)求边AD的长;
(2)设PA=x(m),求S关于x的函数关系式,并指出自变量x的取值范围;
(3)若S=3300m
2,求PA的长.(精确到0.1m)
查看答案和解析>>
科目:
来源:第2章《二次函数》中考题集(50):2.3 二次函数的应用(解析版)
题型:解答题
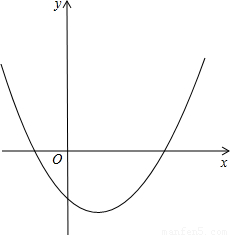
已知:抛物线y=x
2-2x-m(m>0)与y轴交于点C,C点关于抛物线对称轴的对称点为C′点.
(1)求C点,C′点的坐标(可用含m的代数式表示);
(2)如果点Q在抛物线的对称轴上,点P在抛物线上,以点C,C′,P,Q为顶点的四边形是平行四边形,求Q点和P点的坐标(可用含m的代数式表示);
(3)在(2)的条件下,求出平行四边形的周长.
查看答案和解析>>
科目:
来源:第2章《二次函数》中考题集(50):2.3 二次函数的应用(解析版)
题型:解答题
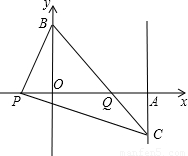
如图,已知平面直角坐标系中三点A(2,0),B(0,2),P(x,0)(x<0),连接BP,过P点作PC⊥PB交过点A的直线a于点C(2,y)
(1)求y与x之间的函数关系式;
(2)当x取最大整数时,求BC与PA的交点Q的坐标.
查看答案和解析>>
科目:
来源:第2章《二次函数》中考题集(50):2.3 二次函数的应用(解析版)
题型:解答题
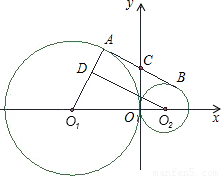
如图,在平面直角坐标系中,半径分别为3
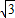
和

的⊙O
1和⊙O
2外切于原点O,在x轴上方的两圆的外公切线AB与⊙O
1和⊙O
2分别切于点A、B,直线AB交y轴于点C.O
2D⊥O
1A于点D.
(1)求∠O
1O
2D的度数;
(2)求点C的坐标;
(3)求经过O
1、C、O
2三点的抛物线的解析式;
(4)在抛物线上是否存在点P,使△PO
1O
2为直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:
来源:第2章《二次函数》中考题集(50):2.3 二次函数的应用(解析版)
题型:解答题
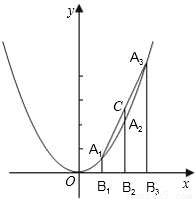
已知A
1、A
2、A
3是抛物线y=

x
2上的三点,A
1B
1、A
2B
2、A
3B
3分别垂直于x轴,垂足为B
1、B
2、B
3,直线A
2B
2交线段A
1A
3于点C.
(1)如图,若A
1、A
2、A
3三点的横坐标依次为1,2,3,求线段CA
2的长;
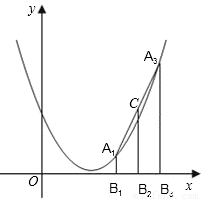
(2)如图,若将抛物线y=

x
2改为抛物线y=

x
2-x+1,A
1、A
2、A
3三点的横坐标为连续整数,其他条件不变,求线段CA
2的长;
(3)若将抛物线y=

x
2改为抛物线y=ax
2+bx+c,A
1、A
2、A
3三点的横坐标为连续整数,其他条件不变,请猜想线段CA
2的长(用a、b、c表示,并直接写出答案).
查看答案和解析>>
科目:
来源:第2章《二次函数》中考题集(50):2.3 二次函数的应用(解析版)
题型:解答题
如图,抛物线y=-x
2+(m+2)x-3(m-1)交x轴于点A、B(A在B的右边),直线y=(m+1)x-3经过点A.若m<1.
(1)求抛物线和直线的解析式;
(2)直线y=kx(k<0)交直线y=(m+1)x-3于点P,交抛物线y=-x
2+(m+2)x-3(m-1)于点M,过M点作x轴垂线,垂足为D,交直线y=(m+1)x-3于点N.问:△PMN能否为等腰三角形?若能,求k的值;若不能,请说明理由.

查看答案和解析>>
科目:
来源:第2章《二次函数》中考题集(50):2.3 二次函数的应用(解析版)
题型:解答题
附加题:若抛物线y=ax2+bx+c(a<0)经过点C(2,3),与x轴交于点M、N,且∠MCN=90°,求a的值.
查看答案和解析>>
科目:
来源:第2章《二次函数》中考题集(50):2.3 二次函数的应用(解析版)
题型:解答题
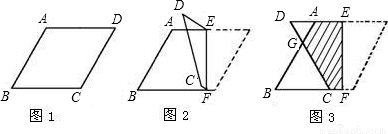
附加题:如图1,菱形纸片ABCD中,AB=1,∠B=60°,将纸片翻折(如图2),使D点落在AD所在直线上,并可在直线AD上运动,折痕为EF.当

<DE<1时,设AB与DC相交于点G(如图).
(1)线段AD与DG相等吗?△ADG与△BCG的面积之和是否随着DE的变化而变化?为什么?
(2)设AD=x,重叠部分(图3中阴影部分)的面积为y,求出y与x之间的函数关系式,并写出自变量x的取值范围以及面积y的取值范围.?
查看答案和解析>>
科目:
来源:第2章《二次函数》中考题集(50):2.3 二次函数的应用(解析版)
题型:解答题
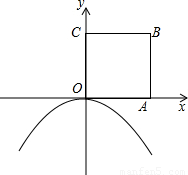
如图所示,边长为1的正方形OABC的顶点A在x轴的正半轴上,将正方形OABC绕点O顺时针旋转30°,使点A落在抛物线y=ax
2(a<0)的图象上.
(1)求抛物线y=ax
2的函数关系式;
(2)正方形OABC继续按顺时针旋转多少度时,点A再次落在抛物线y=ax
2的图象上并求这个点的坐标.
(参考数据:sin30°=

,cos30°=
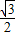
,tan30°=
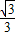
.)
查看答案和解析>>
科目:
来源:第2章《二次函数》中考题集(50):2.3 二次函数的应用(解析版)
题型:解答题
在平面直角坐标系xOy中,已知点A(-1,0),B(0,1),C(2,

).
(Ⅰ)直线l:y=kx+b过A、B两点,求k、b的值;
(Ⅱ)求过A、B、C三点的抛物线Q的解析式;
(Ⅲ)设(Ⅱ)中的抛物线Q的对称轴与x轴相交于点E,那么在对称轴上是否存在点F,使⊙F与直线l和x轴同时相切?若存在,求出点F的坐标;若不存在,请说明理由.
查看答案和解析>>




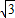 和
和 的⊙O1和⊙O2外切于原点O,在x轴上方的两圆的外公切线AB与⊙O1和⊙O2分别切于点A、B,直线AB交y轴于点C.O2D⊥O1A于点D.
的⊙O1和⊙O2外切于原点O,在x轴上方的两圆的外公切线AB与⊙O1和⊙O2分别切于点A、B,直线AB交y轴于点C.O2D⊥O1A于点D.
 x2上的三点,A1B1、A2B2、A3B3分别垂直于x轴,垂足为B1、B2、B3,直线A2B2交线段A1A3于点C.
x2上的三点,A1B1、A2B2、A3B3分别垂直于x轴,垂足为B1、B2、B3,直线A2B2交线段A1A3于点C. x2改为抛物线y=
x2改为抛物线y= x2-x+1,A1、A2、A3三点的横坐标为连续整数,其他条件不变,求线段CA2的长;
x2-x+1,A1、A2、A3三点的横坐标为连续整数,其他条件不变,求线段CA2的长; x2改为抛物线y=ax2+bx+c,A1、A2、A3三点的横坐标为连续整数,其他条件不变,请猜想线段CA2的长(用a、b、c表示,并直接写出答案).
x2改为抛物线y=ax2+bx+c,A1、A2、A3三点的横坐标为连续整数,其他条件不变,请猜想线段CA2的长(用a、b、c表示,并直接写出答案).


 <DE<1时,设AB与DC相交于点G(如图).
<DE<1时,设AB与DC相交于点G(如图).
 ,cos30°=
,cos30°=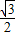 ,tan30°=
,tan30°=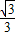 .)
.)
 ).
).