
科目: 来源:第2章《二次函数》中考题集(48):2.3 二次函数的应用(解析版) 题型:解答题
 x2+6的公共点的个数,在图二的情形中通过计算验证你的猜想;如果直线DE与抛物线y=-
x2+6的公共点的个数,在图二的情形中通过计算验证你的猜想;如果直线DE与抛物线y=- x2+6始终有公共点,请在图一中作出这样的公共点.
x2+6始终有公共点,请在图一中作出这样的公共点.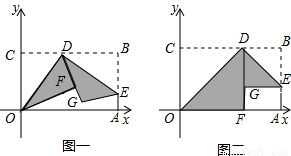
查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(48):2.3 二次函数的应用(解析版) 题型:解答题
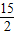 .
.
查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(48):2.3 二次函数的应用(解析版) 题型:解答题
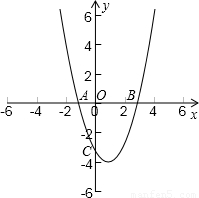
 ),与x轴交于点A、B(A在B的左侧),求∠PAB的度数.
),与x轴交于点A、B(A在B的左侧),求∠PAB的度数.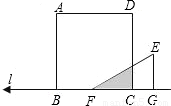

查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(48):2.3 二次函数的应用(解析版) 题型:解答题
 x+1分别交x轴于E,交y轴于F,问△BDC与△EOF是否有可能全等?如果有可能全等请给出证明;如果不可能全等请说明理由.
x+1分别交x轴于E,交y轴于F,问△BDC与△EOF是否有可能全等?如果有可能全等请给出证明;如果不可能全等请说明理由.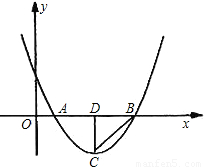
查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(48):2.3 二次函数的应用(解析版) 题型:解答题
 (1)A、B、C、D、E、F、G、H、M9个点中,四个点可以连接成一个四边形,请你用字母写出下列特殊四边形:菱形______;等腰梯形______;平行四边形______;梯形______;(每种特殊四边形只能写一个,写错、多写记0分)
(1)A、B、C、D、E、F、G、H、M9个点中,四个点可以连接成一个四边形,请你用字母写出下列特殊四边形:菱形______;等腰梯形______;平行四边形______;梯形______;(每种特殊四边形只能写一个,写错、多写记0分)查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(48):2.3 二次函数的应用(解析版) 题型:解答题
 x2+bx+c过点A、E,求抛物线的解析式;
x2+bx+c过点A、E,求抛物线的解析式;
查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(48):2.3 二次函数的应用(解析版) 题型:解答题
 x2+kx上,求k的值;
x2+kx上,求k的值;
查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(49):2.3 二次函数的应用(解析版) 题型:解答题
查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(49):2.3 二次函数的应用(解析版) 题型:解答题
 ).
).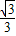 x的图象上,求抛物线的解析式;
x的图象上,求抛物线的解析式;
查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(49):2.3 二次函数的应用(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com