科目： 来源：第2章《二次函数》中考题集（43）：2.3 二次函数的应用（解析版） 题型：解答题

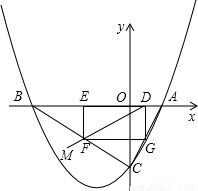
如图：已知抛物线y=x²+x-4与x轴交于A，B两点，与y轴交于点C，O为坐标原点．
（1）求A，B，C三点的坐标；
（2）已知矩形DEFG的一条边DE在AB上，顶点F，G分别在线段BC，AC上，设OD=m，矩形DEFG的面积为S，求S与m的函数关系式，并指出m的取值范围；
（3）当矩形DEFG的面积S取最大值时，连接对角线DF并延长至点M，使FM=DF．试探究此时点M是否在抛物线上，请说明理由．

科目： 来源：第2章《二次函数》中考题集（43）：2.3 二次函数的应用（解析版） 题型：解答题

如图，已知抛物线y=ax²+4ax+t（a＞0）交x轴于A、B两点，交y轴于点C，抛物线的对称轴交x轴于点E，点B的坐标为（-1，0）．
（1）求抛物线的对称轴及点A的坐标；
（2）过点C作x轴的平行线交抛物线的对称轴于点P，你能判断四边形ABCP是什么四边形？并证明你的结论；
（3）连接CA与抛物线的对称轴交于点D，当∠APD=∠ACP时，求抛物线的解析式．

科目： 来源：第2章《二次函数》中考题集（43）：2.3 二次函数的应用（解析版） 题型：解答题

已知：m、n是方程x²-6x+5=0的两个实数根，且m＜n，抛物线y=-x²+bx+c的图象经过点A（m，0）、B（0，n）．
（1）求这个抛物线的解析式；
（2）设（1）中抛物线与x轴的另一交点为C，抛物线的顶点为D，试求出点C、D的坐标和△BCD的面积；
（3）P是线段OC上的一点，过点P作PH⊥x轴，与抛物线交于H点，若直线BC把△PCH分成面积之比为2：3的两部分，请求出P点的坐标．

科目： 来源：第2章《二次函数》中考题集（43）：2.3 二次函数的应用（解析版） 题型：解答题

如图1所示，一张三角形纸片ABC，∠ACB=90°，AC=8，BC=6．沿斜边AB的中线CD把这张纸片剪成△AC₁D₁和△BC₂D₂两个三角形（如图所示）．将纸片△AC₁D₁沿直线D₂B（AB）方向平移（点A，D₁，D₂，B始终在同一直线上），当点D₁于点B重合时，停止平移．在平移过程中，C₁D₁与BC₂交于点E，AC₁与C₂D₂、BC₂分别交于点F、P．
（1）当△AC₁D₁平移到如图3所示的位置时，猜想图中的D₁E与D₂F的数量关系，并证明你的猜想；
（2）设平移距离D₂D₁为x，△AC₁D₁与△BC₂D₂重叠部分面积为y，请写出y与x的函数关系式，以及自变量的取值范围；
（3）对于（2）中的结论是否存在这样的x的值使得y=S_△ABC；若不存在，请说明理由．

科目： 来源：第2章《二次函数》中考题集（43）：2.3 二次函数的应用（解析版） 题型：解答题

在平面直角坐标系内有两点A（-2，0），B（，0），CB所在直线为y=2x+b，
（1）求b与C的坐标；
（2）连接AC，求证：△AOC∽△COB；
（3）求过A，B，C三点且对称轴平行于y轴的抛物线解析式；
（4）在抛物线上是否存在一点P（不与C重合），使得S_△ABP=S_△ABC？若存在，请求出P点坐标；若不存在，请说明理由．

科目： 来源：第2章《二次函数》中考题集（43）：2.3 二次函数的应用（解析版） 题型：解答题

已知抛物线y=ax²+bx+2与x轴相交于点A（x₁，0），B（x₂，0）（x₁＜x₂），且x₁，x₂是方程x²-2x-3=0的两个实数根，点C为抛物线与y轴的交点．
（1）求a，b的值；
（2）分别求出直线AC和BC的解析式；
（3）若动直线y=m（0＜m＜2）与线段AC，BC分别相交于D，E两点，则在x轴上是否存在点P，使得△DEP为等腰直角三角形？若存在，求出点P的坐标；若不存在，说明理由．

科目： 来源：第2章《二次函数》中考题集（43）：2.3 二次函数的应用（解析版） 题型：解答题

如图，在直角坐标系中，O为坐标原点，平行四边形OABC的边OA在x轴上，∠B=60°，OA=6，OC=4，D是BC的中点，延长AD交OC的延长线于点E．
（1）画出△ECD关于边CD所在直线为对称轴的对称图形△E₁CD，并求出点E₁的坐标；
（2）求经过C、E₁、B三点的抛物线的函数表达式；
（3）请探求经过C、E₁、B三点的抛物线上是否存在点P，使以点P、B、C为顶点的三角形与△ECD相似？若存在这样的点P，请求出点P的坐标；若不存在这样的点P，请说明理由．

科目： 来源：第2章《二次函数》中考题集（43）：2.3 二次函数的应用（解析版） 题型：解答题

如图，边长为4的正方形OABC的顶点O为坐标原点，点A在x轴的正半轴上，点C在y轴的正半轴上．动点D在线段BC上移动（不与B，C重合），连接OD，过点D作DE⊥OD，交边AB于点E，连接OE．
（1）当CD=1时，求点E的坐标；
（2）如果设CD=t，梯形COEB的面积为S，那么是否存在S的最大值？若存在，请求出这个最大值及此时t的值；若不存在，请说明理由．

科目： 来源：第2章《二次函数》中考题集（43）：2.3 二次函数的应用（解析版） 题型：解答题

如图抛物线y=，x轴于A、B两点，交y轴于点C，顶点为D．
（1）求A、B、C的坐标；
（2）把△ABC绕AB的中点M旋转180°，得到四边形AEBC：
①求E点坐标；
②试判断四边形AEBC的形状，并说明理由；
（3）试探索：在直线BC上是否存在一点P，使得△PAD的周长最小？若存在，请求出P点的坐标；若不存在，请说明理由．

科目： 来源：第2章《二次函数》中考题集（43）：2.3 二次函数的应用（解析版） 题型：解答题

如图，直线y=-x+2与x轴交于点C，与y轴交于点B，点A为y轴正半轴上的一点，⊙A经过点B，O，直线BC交⊙A于点D．
（1）求点D的坐标．
（2）以OC为直径作⊙O'，连接AD，直线AD与⊙O'相切吗？为什么？
（3）过O，C，D三点作抛物线，在抛物线的对称轴上是否存在一点P，使线段PO与PD之差的值最大？若存在，请求出这个最大值和点P的坐标，若不存在，请说明理由．