相关习题
0 127025 127033 127039 127043 127049 127051 127055 127061 127063 127069 127075 127079 127081 127085 127091 127093 127099 127103 127105 127109 127111 127115 127117 127119 127120 127121 127123 127124 127125 127127 127129 127133 127135 127139 127141 127145 127151 127153 127159 127163 127165 127169 127175 127181 127183 127189 127193 127195 127201 127205 127211 127219 366461
科目:
来源:第2章《二次函数》中考题集(40):2.3 二次函数的应用(解析版)
题型:解答题
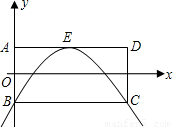
已知矩形ABCD中,AB=2,AD=4,以AB的垂直平分线为x轴,AB所在的直线为y轴,建立平面直角坐标系(如图).
(1)写出A,B,C,D及AD的中点E的坐标;
(2)求以E为顶点、对称轴平行于y轴,并且经过点B,C的抛物线的解析式;
(3)求对角线BD与上述抛物线除点B以外的另一交点P的坐标;
(4)△PEB的面积S
△PEB与△PBC的面积S
△PBC具有怎样的关系?证明你的结论.
查看答案和解析>>
科目:
来源:第2章《二次函数》中考题集(40):2.3 二次函数的应用(解析版)
题型:解答题
如图,在平面直角坐标系中,正方形AOCB的边长为1,点D在x轴的正半轴上,且OD=OB,BD交OC于点E.
(1)求∠BEC的度数;
(2)求点E的坐标;
(3)求过B,O,D三点的抛物线的解析式.

查看答案和解析>>
科目:
来源:第2章《二次函数》中考题集(40):2.3 二次函数的应用(解析版)
题型:解答题
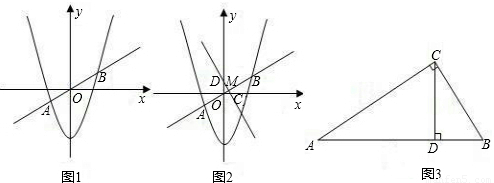
如图1,在平面直角坐标系中,抛物线
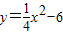
与直线

相交于A,B两点.
(1)求线段AB的长;
(2)若一个扇形的周长等于(1)中线段AB的长,当扇形的半径取何值时,扇形的面积最大,最大面积是多少;
(3)如图2,线段AB的垂直平分线分别交x轴、y轴于C,D两点,垂足为点M,分别求出OM,OC,OD的长,并验证等式
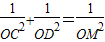
是否成立;
(4)如图3,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,设BC=a,AC=b,AB=c.CD=b,试说明:

.
查看答案和解析>>
科目:
来源:第2章《二次函数》中考题集(40):2.3 二次函数的应用(解析版)
题型:解答题
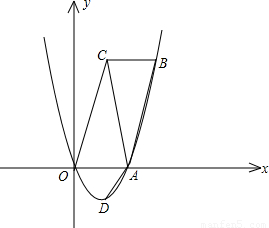
如图,在平面直角坐标系xOy中,O为原点,点A、C的坐标分别为(2,0)、(1,
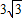
).将△AOC绕AC的中点旋转180°,点O落到点B的位置,抛物线y=ax
2-2

x经过点A,点D是该抛物线的顶点.
(1)求证:四边形ABCO是平行四边形;
(2)求a的值并说明点B在抛物线上;
(3)若点P是线段OA上一点,且∠APD=∠OAB,求点P的坐标;
(4)若点P是x轴上一点,以P、A、D为顶点作平行四边形,该平行四边形的另一顶点在y轴上,写出点P的坐标.
查看答案和解析>>
科目:
来源:第2章《二次函数》中考题集(40):2.3 二次函数的应用(解析版)
题型:解答题
关于x的二次函数y=-x2+(k2-4)x+2k-2以y轴为对称轴,且与y轴的交点在x轴上方.
(1)求此抛物线的解析式,并在下面建立直角坐标系画出函数的草图;
(2)设A是y轴右侧抛物线上的一个动点,过点A作AB垂直于x轴于点B,再过点A作x轴的平行线交抛物线于点D,过点D作DC垂直于x轴于点C,得到矩形ABCD.设矩形ABCD的周长为l,点A的横坐标为x,试求l关于x的函数关系式;
(3)当点A在y轴右侧的抛物线上运动时,矩形ABCD能否成为正方形?若能,请求出此时正方形的周长;若不能,请说明理由.
查看答案和解析>>
科目:
来源:第2章《二次函数》中考题集(40):2.3 二次函数的应用(解析版)
题型:解答题
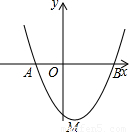
如图,抛物线y=x
2-2x-3与x轴分别交于A,B两点.
(1)求A,B两点的坐标;
(2)求抛物线顶点M关于x轴对称的点M′的坐标,并判断四边形AMBM′是何特殊平行四边形.(不要求说明理由)
查看答案和解析>>
科目:
来源:第2章《二次函数》中考题集(40):2.3 二次函数的应用(解析版)
题型:解答题
已知抛物线y=x2+4x+m(m为常数)经过点(0,4)
(1)求m的值;
(2)将该抛物线先向右、再向下平移得到另一条抛物线.已知这条平移后的抛物线满足下述两个条件:它的对称轴(设为直线l2)与平移前的抛物线的对称轴(设为l1)关于y轴对称;它所对应的函数的最小值为-8.
①试求平移后的抛物线所对应的函数关系式;
②试问在平移后的抛物线上是否存在着点P,使得以3为半径的⊙P既与x轴相切,又与直线l2相交?若存在,请求出点P的坐标,并求出直线l2被⊙P所截得的弦AB的长度;若不存在,请说明理由.
查看答案和解析>>
科目:
来源:第2章《二次函数》中考题集(41):2.3 二次函数的应用(解析版)
题型:解答题
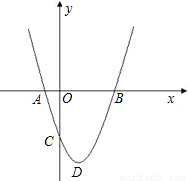
如图,顶点为D的抛物线y=x
2+bx-3与x轴相交于A、B两点,与y轴相交于点C,连接BC,已知tan∠ABC=1.
(1)求点B的坐标及抛物线y=x
2+bx-3的解析式;
(2)在x轴上找一点P,使△CDP的周长最小,并求出点P的坐标;
(3)若点E(x,y)是抛物线上不同于A,B,C的任意一点,设以A,B,C,E为顶点的四边形的面积为S,求S与x之间的函数关系式.
查看答案和解析>>
科目:
来源:第2章《二次函数》中考题集(41):2.3 二次函数的应用(解析版)
题型:解答题
如图,抛物线y=x
2+bx-c经过直线y=x-3与坐标轴的两个交点A,B,此抛物线与x轴的另一个交点为C,抛物线的顶点为D.
(1)求此抛物线的解析式;
(2)点P为抛物线上的一个动点,求使S
△APC:S
△ACD=5:4的点P的坐标.

查看答案和解析>>
科目:
来源:第2章《二次函数》中考题集(41):2.3 二次函数的应用(解析版)
题型:解答题
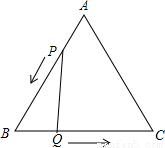
已知:如图,△ABC是边长3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动.设点P的运动时间为t(s),解答下列问题:
(1)当t为何值时,△PBQ是直角三角形?
(2)设四边形APQC的面积为y(cm
2),求y与t的关系式;是否存在某一时刻t,使四边形APQC的面积是△ABC面积的三分之二?如果存在,求出相应的t值;不存在,说明理由;
(3)设PQ的长为x(cm),试确定y与x之间的关系式.
查看答案和解析>>



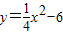 与直线
与直线 相交于A,B两点.
相交于A,B两点.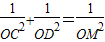 是否成立;
是否成立; .
.
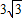 ).将△AOC绕AC的中点旋转180°,点O落到点B的位置,抛物线y=ax2-2
).将△AOC绕AC的中点旋转180°,点O落到点B的位置,抛物线y=ax2-2 x经过点A,点D是该抛物线的顶点.
x经过点A,点D是该抛物线的顶点.



