
科目: 来源:第2章《二次函数》中考题集(32):2.3 二次函数的应用(解析版) 题型:解答题
 .
.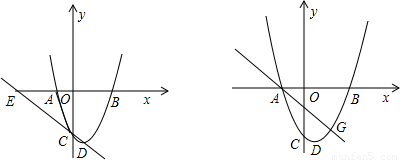
查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(32):2.3 二次函数的应用(解析版) 题型:解答题
 ,β=
,β= ,求函数y2的解析式;
,求函数y2的解析式;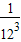 时,求t的值;
时,求t的值;查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(32):2.3 二次函数的应用(解析版) 题型:解答题
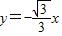 +m与x轴交于点E.
+m与x轴交于点E.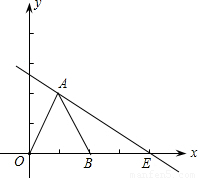
查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(32):2.3 二次函数的应用(解析版) 题型:解答题
 x+1交坐标轴于A,B两点,以线段AB为边向上作正方形ABCD,过点A,D,C的抛物线与直线另一个交点为E.
x+1交坐标轴于A,B两点,以线段AB为边向上作正方形ABCD,过点A,D,C的抛物线与直线另一个交点为E.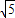 个单位长度的速度沿射线AB下滑,直至顶点D落在x轴上时停止.设正方形落在x轴下方部分的面积为S,求S关于滑行时间t的函数关系式,并写出相应自变量t的取值范围;
个单位长度的速度沿射线AB下滑,直至顶点D落在x轴上时停止.设正方形落在x轴下方部分的面积为S,求S关于滑行时间t的函数关系式,并写出相应自变量t的取值范围;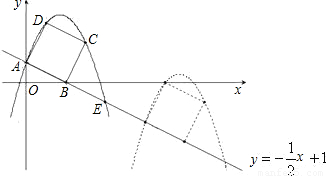
查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(32):2.3 二次函数的应用(解析版) 题型:解答题
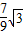 ),且顶点C的横坐标为4,该图象在x轴上截得的线段AB的长为6.
),且顶点C的横坐标为4,该图象在x轴上截得的线段AB的长为6.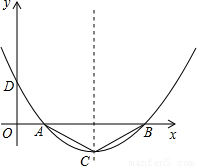
查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(32):2.3 二次函数的应用(解析版) 题型:解答题
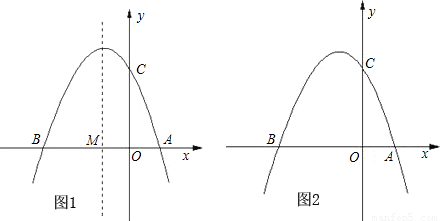
查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(32):2.3 二次函数的应用(解析版) 题型:解答题
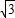 ,∠OBA=90°.以边OB所在直线折叠Rt△OAB,使点A落在点C处.
,∠OBA=90°.以边OB所在直线折叠Rt△OAB,使点A落在点C处. 时,过点A作AM⊥PD于点M,若k=
时,过点A作AM⊥PD于点M,若k=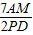 ,求证:二次函数y=-2x2-(7k-3
,求证:二次函数y=-2x2-(7k-3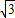 )x+
)x+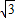 k的图象关于y轴对称.
k的图象关于y轴对称.
查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(33):2.3 二次函数的应用(解析版) 题型:解答题
查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(33):2.3 二次函数的应用(解析版) 题型:解答题
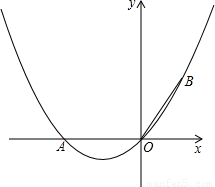
 x2-
x2- x+
x+ ,经过变换后,AC=2
,经过变换后,AC=2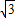 ,点P是直线AC上的动点,求点P到点D的距离和到直线AD的距离之和的最小值.
,点P是直线AC上的动点,求点P到点D的距离和到直线AD的距离之和的最小值.查看答案和解析>>
科目: 来源:第2章《二次函数》中考题集(33):2.3 二次函数的应用(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com